Question
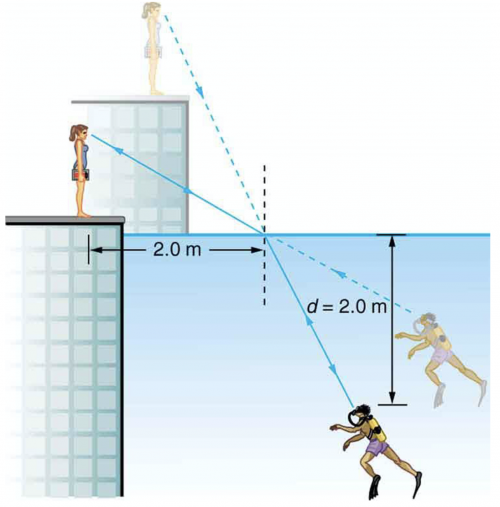
(a) Given that the angle between the ray in the water and the perpendicular to the water is , and using information in Figure 25.53, find the height of the instructor’s head above the water, noting that you will first have to calculate the angle of incidence. (b) Find the apparent depth of the diver’s head below water as seen by the instructor.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 25, Problem 12 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
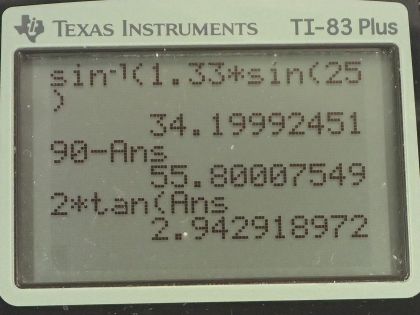
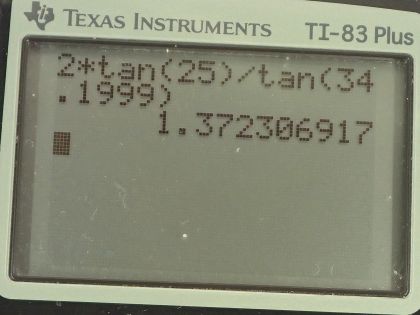
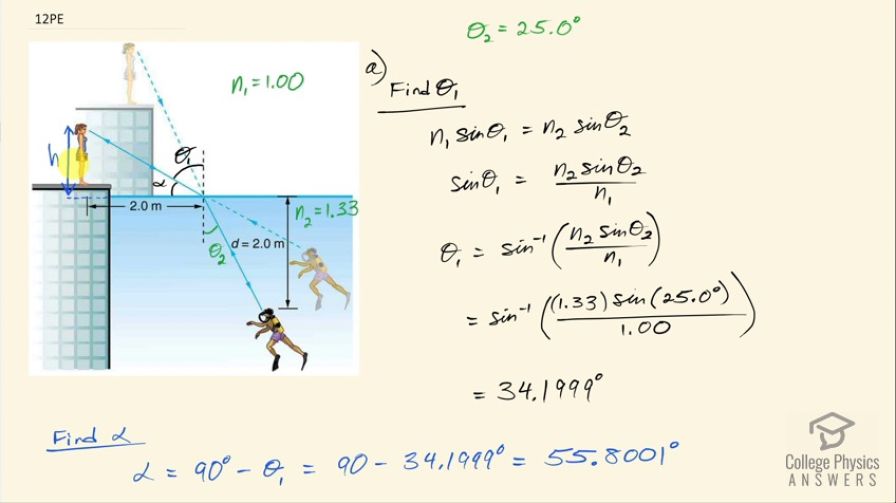
This is College Physics Answers with Shaun Dychko. A swimming instructor is standing on a pool deck some height above the water line and this arrow intentionally goes a bit below the floor to the level of the water and we have to figure out what this height is between the water level and the eyes of the instructor. So the ray going from her eyes to the water and then to the diver, it refracts at this air-water interface and we are given the angle between the ray and the perpendicular in the water that's Θ 2 and Θ 2 is 25.0 degrees. We know the index of refraction of water, which we can look up in in the table in the textbook and it's 1.33; the index of refraction for air is 1.00. So to find this height between the water level and the instructor's eyes, we are first going to figure out what is this angle Θ 1—and we can use Snell's law to do that— and then knowing that angle, we'll figure out what α is because α and this angle Θ 1 are complementary— they add up to 90— and we know this side of this triangle here... this triangle... its side length is 2.00 meters so horizontally, the instructor is standing 2.00 meters from this point of contact between the ray and the water and then we can use trigonometry to figure out the height h... okay and that's part (a). So first find Θ 1 and Snell's law says the first index of refraction times sin of the first angle measured between the perpendicular and the ray is equal to the second index of refraction times sin of the second angle measured between the ray and the perpendicular. So we'll solve for sin Θ 1 by dividing both sides by n 1 and then take the inverse sin of both sides to solve for Θ 1 so Θ 1 is the inverse sin of n 2sin Θ 2 over n 1. So that's the inverse sin of 1.33— index of refraction of water— times sin of 25.0 degrees divided by 1 and that's 34.1999 degrees. Then we want to know α and so α is this full 90 minus the Θ 1 and so that works out to 55.8001 degrees and the tangent of α is this opposite divided by the adjacent— this is a right triangle here— and so tan of α is h over 2.0 meters and we multiply both sides by 2.0 meters to solve for h. So the height then is 2.0 meters times tan of 55.8001 degrees and that's 2.94 meters. Okay! Part (b) is asking what is the depth below the water line of the diver's image? So the apparent depth according to the instructor's perspective... what is this d prime—we'll call it— this depth below the water line of the image of the diver? We are told by the question to assume that the diver's image and the diver's object are the same horizontal distance from this perpendicular. According to the picture they are not but in order to be able to answer the question, we have to assume that they are the same distance so this is distance x and this is also distance x— you have to imagine that this is actually positioned just here. Okay! So we have a triangle with a vertical height of d— that's the depth below the water for the object— and then we have this horizontal distance from the perpendicular x and then there's this angle Θ 2, which we are given 25.0 degrees so I am just redrawing this triangle here here and then we also have this triangle d prime— the depth of the image— and then this horizontal is the same— horizontal distance from the perpendicular x— and then we have this angle Θ 1 because this angle here between the image and the perpendicular is opposite to this angle here between the perpendicular and this ray going to the instructor's eyes and so these angles are the same so this is Θ 1 here. And then we can say tan of Θ 2 is x divided by d and tan of Θ 1 is x divided by d prime and we want to figure out what d prime is so let's first replace x based on this equation So this equation goes here and we solve for x by multiplying both sides by d So the horizontal distance between the image or object and the perpendicular is the depth of the object times tan of Θ 2 and we replace x in this equation with dtan Θ 2 here and then we can solve for d prime by multiplying both sides by d prime over tan Θ 1. So the depth of the image then is the depth of the diver itself multiplied by tan Θ 2 divided by tan Θ 1. So that's 2.0 meters times tan of 25.0 degrees divided by tan of 34.1999 degrees— as we figured out way back here in part (a)— and this works out to 1.37 meters is the depth of the diver's image.