Question
Suppose your 50.0 mm focal length camera lens is 51.0 mm away from the film in the camera. (a) How far away is an object that is in focus? (b) What is the height of the object if its image is 2.00 cm high?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 25, Problem 46 (Problems & Exercises)
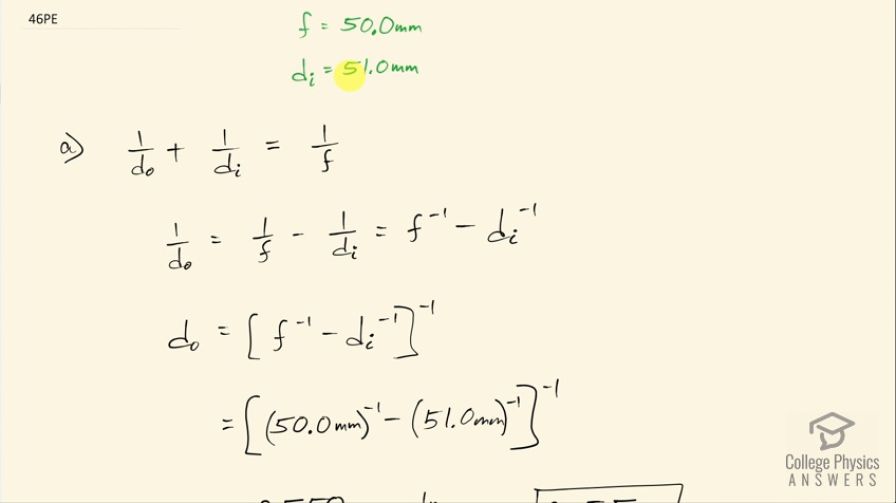
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A camera has a 50.0 millimeter focal length lens in it and it's projecting the image a distance 51.0 millimeters away from the lens and the question is where is the object or the subject of the photo located? So that is d o in other words that we want to find... the object distance. So this is the thin lens equation: 1 over the object distance plus 1 over the image distance equals 1 over the focal length and we'll first subtract 1 over d i from both sides and we get 1 over the object distance is 1 over f minus 1 over d i. I prefer to write this 1 over business as the denominator to the power of negative 1 because this exponent negative 1 means take the reciprocal of this and so f to the power of negative 1 is 1 over f and I prefer to write it this way with this exponent because the calculator conveniently has a button, which says exponent negative 1. So we have f to the negative 1 minus d i to the negative 1 equals this. So then we raise both sides to the exponent negative 1 to solve for d o. And so we have object distance then is f to the negative 1 minus d i to the negative 1 all to the negative 1. So 50.0 millimeters to the negative 1 minus 51.0 millimeters to the negative 1 and then take that difference and then the result is raised to the exponent negative 1, we get 2550 and this is units of millimeters because those are the units we are working with here and we want to change that into meters by multiplying by 1 meter for every 1000 millimeters and this gives us 2.55 meters is the distance to the object. Part (b) asks us what is the height of the object if its image is 2.00 centimeters high? So magnification is the ratio of the image height to the object height and we are gonna be solving for h o here, this magnification is also the negative of the image distance divided by the object distance so we can solve for h o by multiplying both sides by h od o over d i negative so times negative h od o over d i. So the h o cancels on the left side and the d i and the d o cancels on the right side and the negative becomes positive on the right side and then switch the sides around and we have h o equals negative h id o over d i. Now I am plugging in numbers here and I am kind of asking for trouble in a way... you know, I wanted to draw attention to the fact that I have mixed units in this work here, which you can do so long as you are doing it with a lot of attention. So I can mix the millimeters and the centimeters only because I know the millimeters here— the object distance which I wrote in the millimeters, 2550 millimeters— I am dividing it by a different number also in millimeters— this image distance is 51.0 millimeters. So because I am dividing millimeters by millimeters, I know that those millimeters are gonna cancel and this portion of the fraction is going to be dimensionless because the millimeters divided by the millimeters mean there are no units and so then that fraction gets multiplied by the dimensions here, which is centimeters and so our answer will be in units of centimeters. If all of this... you are not comfortable with then you should the traditional, sort-of change everything to meters— which is what we normally do— and then switch back into whatever units you want in the final answer. Okay! So we have negative of 2.00 centimeters times 2550 millimeters divided by 51.0 millimeters and this works out to negative 100 centimeters and this negative sign means the orientation of the object will be opposite to the orientation of the image.
