Question
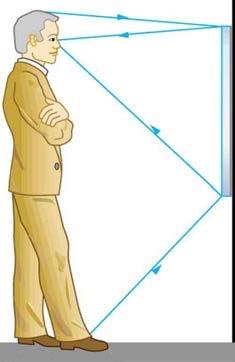
Suppose a man stands in front of a mirror as shown in Figure 25.49. His eyes are 1.65 m above the floor, and the top of his head is 0.13 m higher. Find the height above the floor of the top and bottom of the smallest mirror in which he can see both the top of his head and his feet. How is this distance related to the man’s height?
<b>Figure 25.49</b> A full-length mirror is one in which you can see all of yourself. It need not be as big as you, and its size is independent of your distance from it.
Figure 25.49 A full-length mirror is one in which you can see all of yourself. It need not be as big as you, and its size is independent of your distance from it.
Question by OpenStax is licensed under CC BY 4.0
Final Answer

hb=0.825 mh_\textrm{b} = 0.825 \textrm{ m}
ht=1.72 mh_\textrm{t} = 1.72 \textrm{ m}
Note: The man's height affects the answer: the height of the bottom of the mirror is half the distance from the man's eyes and the ground, whereas the top of the mirror height is the height of the man's eyes plus half the distance between the man's eyes and top of his head.

Solution video

OpenStax College Physics for AP® Courses, Chapter 25, Problem 1 (Problems & Exercises)

vote with a rating of votes with an average rating of .
Select problem
Next Chevron right

Calculator Screenshots

  • OpenStax College Physics, Chapter 25, Problem 1 (PE) calculator screenshot 1