Question
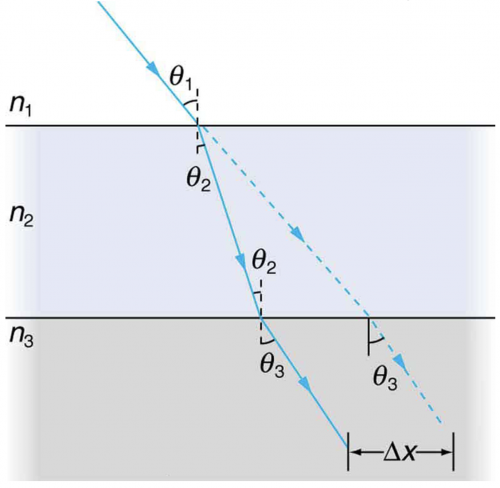
Figure 25.54 shows a ray of light passing from one medium into a second and then a third. Show that is the
same as it would be if the second medium were not present (provided total internal reflection does not occur).
Final Answer
Please see the solution video.
Solution video
OpenStax College Physics for AP® Courses, Chapter 25, Problem 16 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
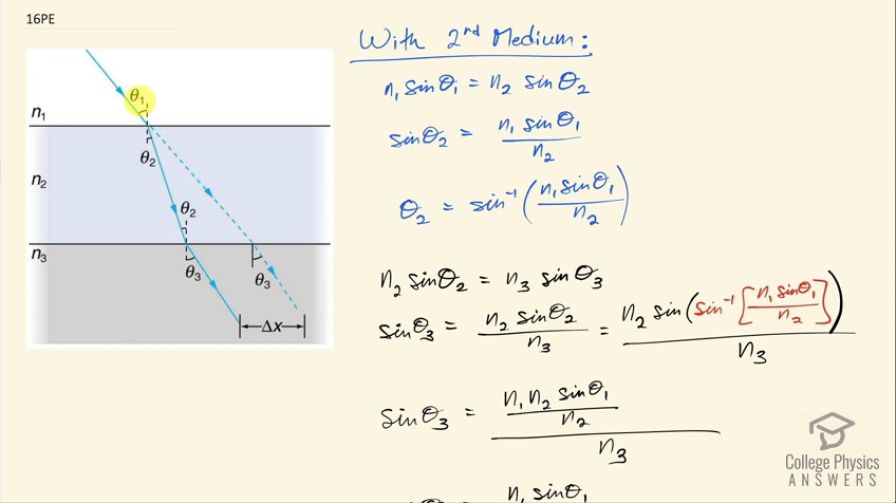
This is College Physics Answers with Shaun Dychko. There is a ray that is going through medium number one initially, it has some incident angle Θ 1 with respect to this perpendicular and then it enters medium number two, which must have a higher index of refraction to make this ray refract towards the normal and then eventually, it passes through medium number two and then refracts again at this interface with medium number three and it emerges in medium three with this angle Θ 3 with respect to this perpendicular. We are going to show that this angle Θ 3 is the same regardless of whether or not the ray encounters this medium number two— this medium number two has no effect on what Θ 3 will be; it's only dependent on n 1Θ 1 and n 3Θ 3. So we are gonna show that by first figuring out what Θ 3 is with medium number two—let's suppose that medium number two does matter— and we'll first figure out what this angle Θ 2 is using Snell's law applied to this interface between medium number one and number two and then figure out Θ 2 and then use that Θ 2 with Snell's law again at this interface and figure out what Θ 3 would be and then we'll compare that to an analysis where we have only medium one and medium three. So figuring out Θ 2 first of all, we have n 1sin Θ 1 equals n 2sin Θ 2— that's Snell's law at this interface— we'll divide both sides by n 2 and then switch the sides around and we have sin Θ 2 equals n 1sin Θ 1 over n 2 then we can take the inverse sin of both sides to figure out Θ 2 and we don't need to know what the number is, we just need to know this expression. So then we turn our attention to the interface between medium two and three and apply Snell's law there and that says n 2sin Θ 2 equals n 3sin Θ 3 and we'll solve for Θ 3 by first dividing both sides by n 3 and then we get an expression for sin Θ 3: it equals n 2sin Θ 2 over n 3 and then we'll substitute Θ 2 into this sin function so Θ 2 is the inverse sin of n 1sin Θ 1 over n 2 so taking the sin of the inverse sin just gives us the argument so the sin is the opposite of the inverse sin and you are just left with this thing that's being taken the inverse sin of. So this n 1sin Θ 1 over n 2 is here multiplied by n 2. So this is n 1sin Θ 1 over n 2—came from this argument of the inverse sin function— and this n 2 is here. Okay! And we see that the n 2's cancel and we are left with n 1sin Θ 1 over n 3 and already this is enough for us to conclude that the medium number two doesn't matter because nothing about medium two is in this expression so the sin of this Θ 3 depends only on n 1, n 3 and sin of Θ 1. But let's do the analysis again anyway without the second layer and we have Snell's law for an interface between medium one and medium three where we have the same incident angle as before and then we'll have some other angle that we will call Θ 3 prime giving it a prime to distinguish it from the Θ 3 here on the assumption that it might be different. So we have n 3sin Θ 3 prime equals n 1sin Θ 1 and that means that sin Θ 3 prime is n 1sin Θ 1 over n 3 after you divide both sides by n 3 here. And so we see that sin Θ 3 prime is the same as sin Θ 3 because sin Θ 3 is this expression, sin Θ 3 prime is the exact same expression— n 1sin Θ 1 over n 3 in other words— and so that means these angles must be the same since the sin of them is the same and there we are... the angle is the same regardless of the presence of the second layer.