Question
Light shows staged with lasers use moving mirrors to swing beams and create colorful effects. Show that a light ray reflected from a mirror changes direction by when the mirror is rotated by an angle .
Final Answer
Please see the solution video.
Solution video
OpenStax College Physics for AP® Courses, Chapter 25, Problem 3 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
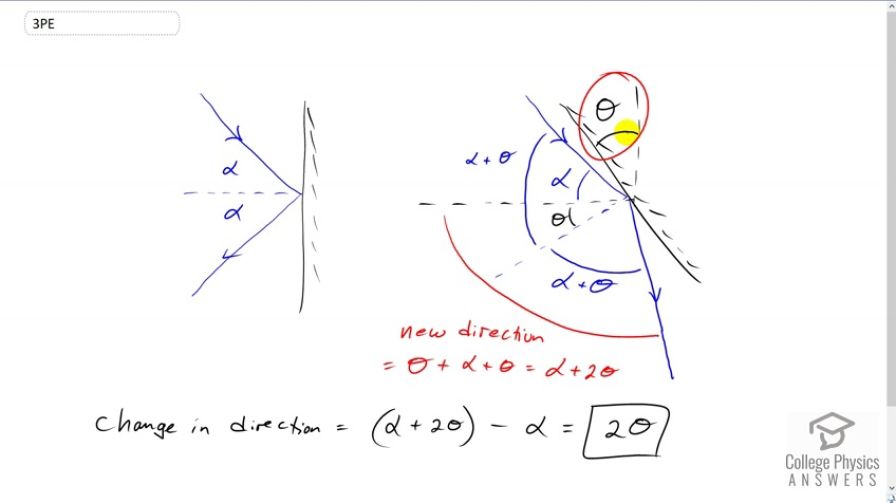
This is College Physics Answers with Shaun Dychko. We're going to show that when a ray hits a flat mirror and that mirror is rotated by an angle of theta degrees the direction of the ray will change by two times that angle. So, we have this picture here initially and the ray is going to an angle of alpha with respect to this dotted line here. And then later on, we're going to show that the ray is going at an angle of theta plus alpha plus theta or alpha plus two theta with respect to the same horizontal dotted line. So, after the mirror is rotated by an angle theta, the ray is still incident at the same angle as it was before. But now, it has a new angle with respect to the perpendicular of the mirror. So, this is the new perpendicular of the mirror in blue here and here's the old perpendicular to the mirror. And, this perpendicular or normal, you might say, has moved by an angle theta because it's attached to the mirror, of course. And now, the new angle of incidence is this total alpha, the angle with respect to the original perpendicular plus this new theta. So, the angle of incidence is alpha plus theta. And so, the angle of reflection has to be the same, alpha plus theta. And so, the question is what is the new direction of the ray with respect to the original perpendicular? So, that's going to be this alpha plus theta that we found here plus this additional theta. And so, that's alpha plus two theta. And so, the change in direction is the new angle, which is alpha plus two theta minus the original angle of theta and then that makes the difference of two theta.