Question
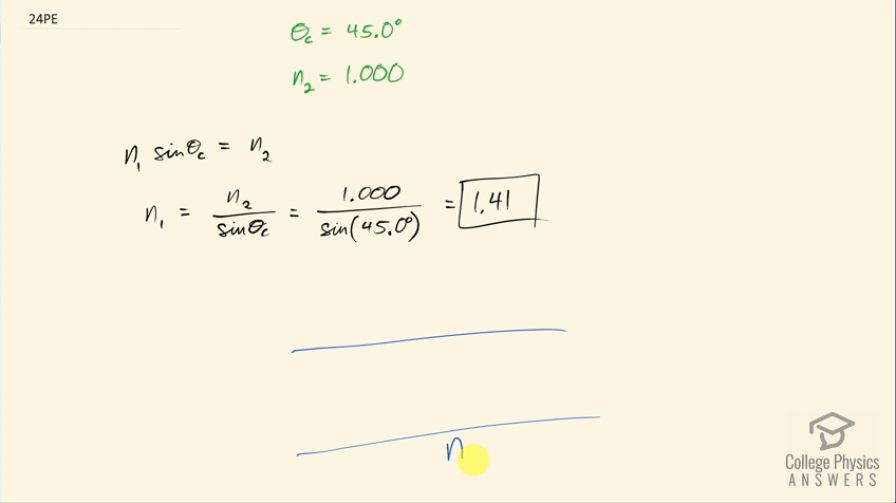
Suppose you are using total internal reflection to make an efficient corner reflector. If there is air outside and the incident angle is , what must be the minimum index of refraction of the material from which the reflector is made?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 25, Problem 24 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
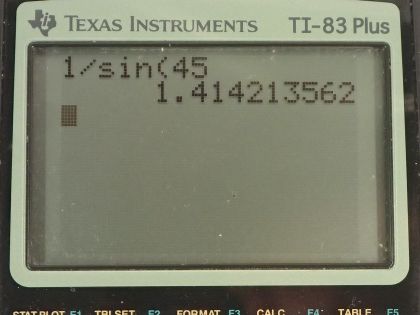
Video Transcript
This is College Physics Answers with Shaun Dychko. We want to choose some kind of material such that when there's air on one side of the material, there's going to be total internal reflection when there's an incident angle of a light beam at 45.0 degrees. So this should be the critical angle... is 45.0 degrees in other words and this beam of light will you know this is basically where it will refract such that it's perpendicular or it's just the border beyond which there's total internal reflection. So if you apply Snell's law to this interface, you will say that n 1 times sin of the incident angle equals n 2 times sin of the refracted angle but the refracted angle will be 90 degrees and so sin of 90 is 1, which is why this is the expression for Snell's law when you have a critical angle, there's no sin thing here because it's just the number one. We want to solve for n 1—the index of refraction of this unknown material. So we divide both sides by sin of the critical angle so n 1 then is the index of refraction of the second medium, which is air in this case which has an index of refraction of 1.000 and divide that by sin of the critical angle of 45.0 degrees and this is 1.41 is the minimum index of refraction needed for this material to have total internal reflection when there's an incident angle of 45.0 degrees.