Question
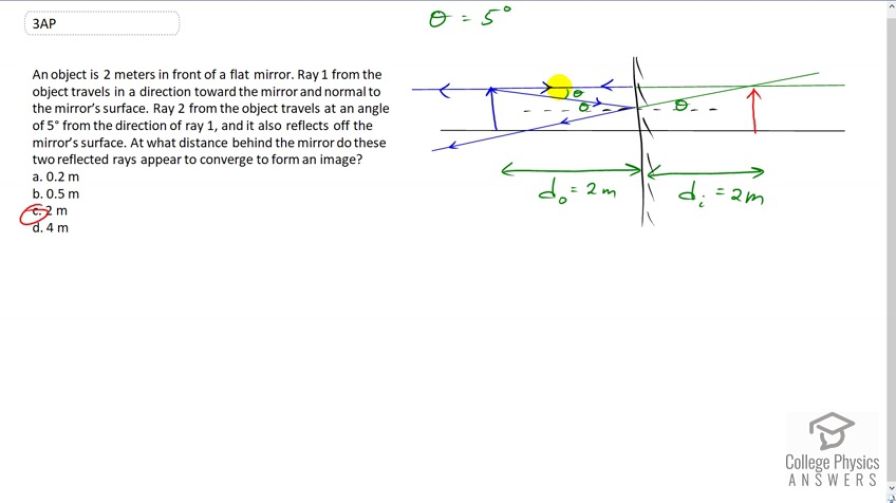
An object is 2 meters in front of a flat mirror. Ray 1 from the object travels in a direction toward the mirror and normal to the mirror’s surfacRay 2 from the object travels at an angle of 5° from the direction of ray 1, and it also reflects off the mirror’s surfacAt what distance behind the mirror do these two reflected rays appear to converge to form an image?
- 0.2 m
- 0.5 m
- 2 m
- 4 m
Final Answer
(c)
Solution video
OpenStax College Physics for AP® Courses, Chapter 25, Problem 3 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. An object is two meters in front of a flat mirror and Ray one is traveling normal to the mirror. And so it's angle of incidence is going to be the same of as it’s angle of reflection. And so it's going to bounce straight back at also at 90 degrees. And then Ray two is going at an angle five degrees with respect to the first Ray and it'll hit the mirror and then bounce-off with the same angle of reflection as it had for the angle of incidence. So the angle of incidence is five degrees and this dotted line is a normal to the mirror 90 degrees to the mirror and this angle between the normal and the ray is, these are interior opposite angles between parallel lines Ray one being parallel to this normal here. And so these angles here are both Theta. So this Theta is in here and this Theta is there. And then we're going to show that these two triangles are congruent by the way. This is what we're building up to here this triangle and this triangle are congruent and we're going to show that by the angle-side-angle rule and then after knowing that they're congruent we can then conclude that the image distance must be the same as the object distance because corresponding sides are equal in congruent triangles. So we can establish that this angle equals this angle in the green and blue triangles because they're both 90 degrees and then they share this common side. So those sides are equal between the two triangles and then we have to show that this angle here equals this angle here. And now given that this is Theta this is an opposite angle to this one. And so it's also Theta . And now this angle which you might call Red Dot angle plus Theta has to make 90 on this side and likewise on the other side the Red Dot plus Theta has to make 90. And so that means these two angles these red dots angles are the same and so these triangles are therefore congruent and because the congruent corresponding sides are equal and so the side opposite the Red Dot angle have to be equal and so the image distance then because that's what this side represents, the image distance is there for two meters behind the mirror.