Question
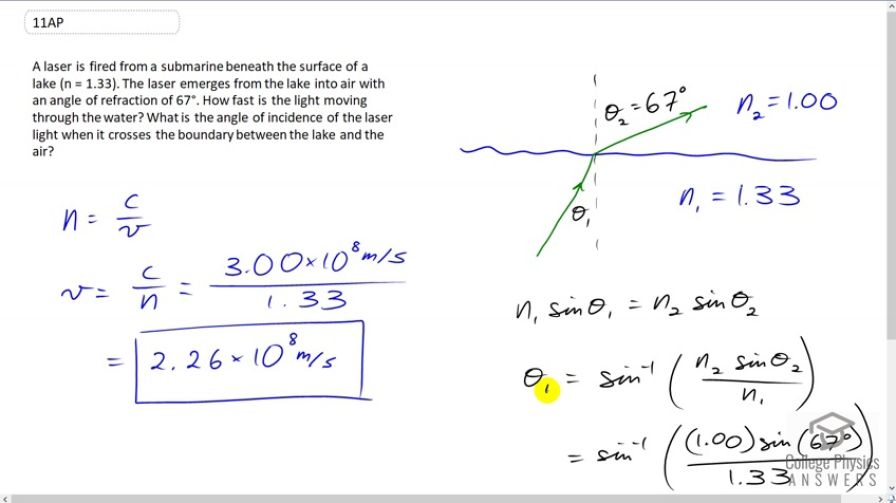
A laser is fired from a submarine beneath the surface of a lake (n = 1.33). The laser emerges from the lake into air with an angle of refraction of . How fast is the light moving through the water? What is the angle of incidence of the laser light when it crosses the boundary between the lake and the air?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 25, Problem 11 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
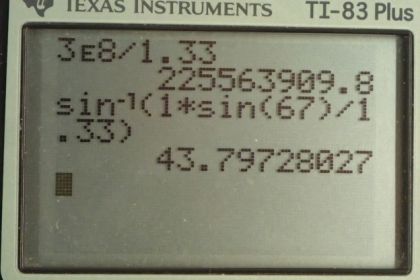
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A submarine is firing a laser below the surface of the water at some angle of incidence, theta one that we're going to calculate in a second. And then, it emerges into the air at an angle of refraction, theta two 67 degrees. So, the index of refraction in air is 1.00 and that in water is 1.33. And so, from the index of refraction, we can figure out the speed of the laser through the water. And, it's going to be speed of light in the vacuum divided by speed in water. And, we'll multiply both sides by V over N to solve for V. And, we have the speed in the water is speed of light in the vacuum divided by the index of refraction. So, that's 3.00 times ten to the eight meters per second divided by 1.33 which gives the speed of 2.26 times ten to the eight meters per second in the water. Now,what angle of incidence must there have been in order to have this angle of refraction? Well, Snell's law says that the initial medium index of refraction times sine of the incidence angle equals the final index of refraction times sine of the angle of refraction. So, we can divide both sides by N one and then take the inverse sine of both sides and we have the incident angle is inverse sine of N two sine theta two over N one. So, that's the inverse sine of the index of refraction of air times sine of 67 degrees angle of refraction divided by the index of refraction of water, which is where it began, which is 1.33, giving an angle of incidence of 44 degrees.