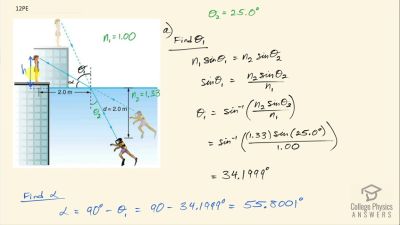
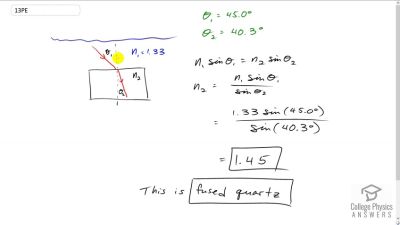
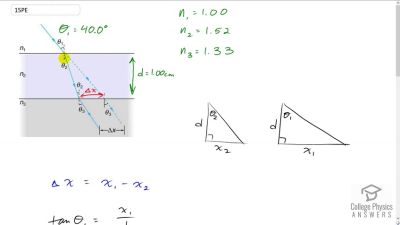
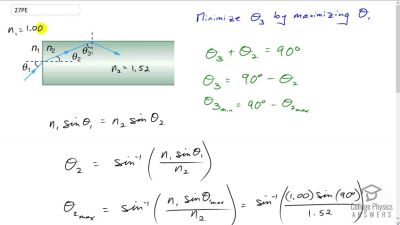
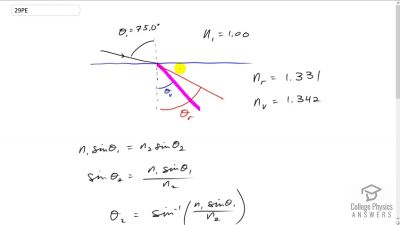
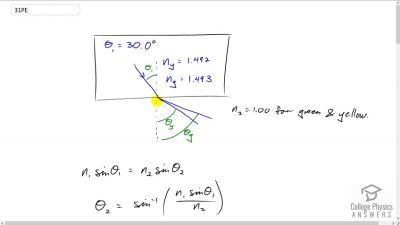
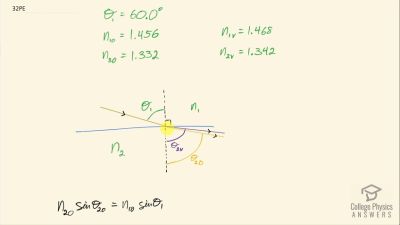
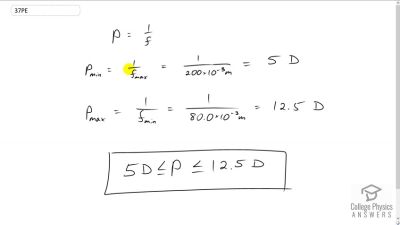
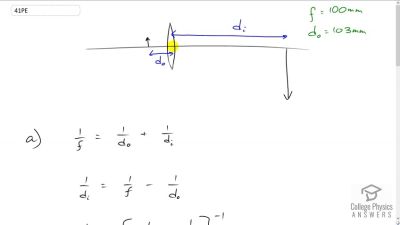
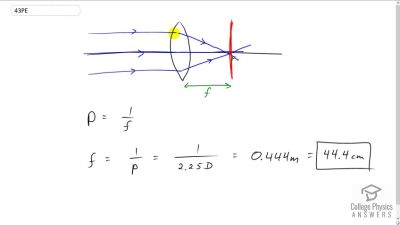
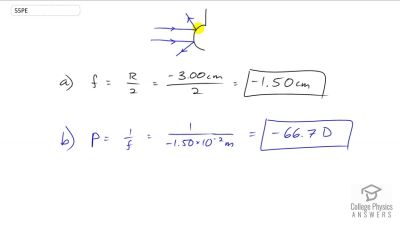
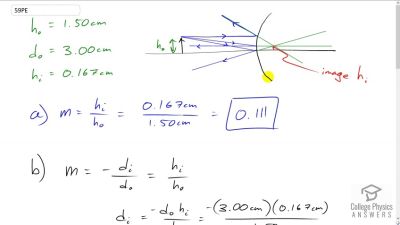
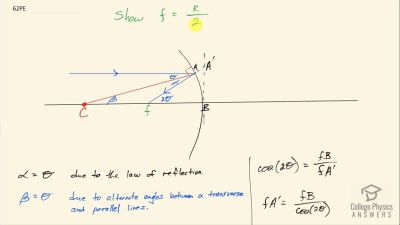
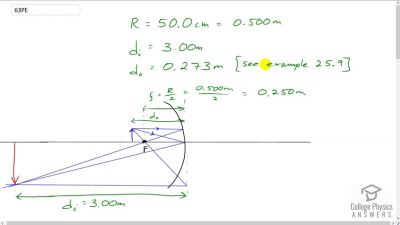
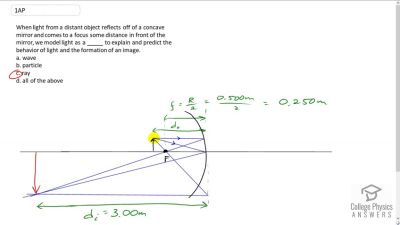
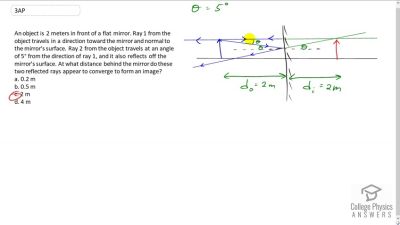
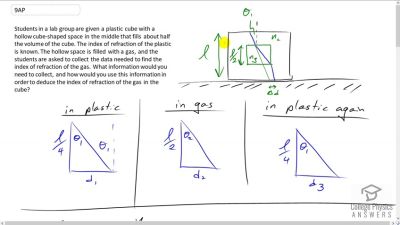
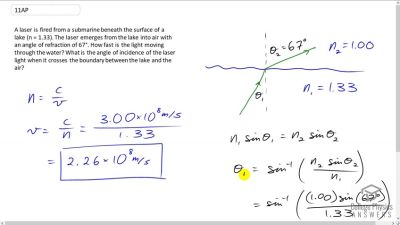
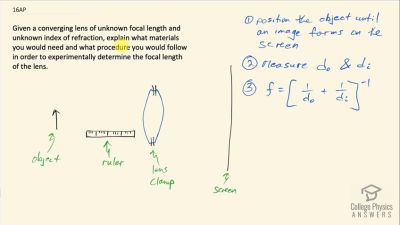
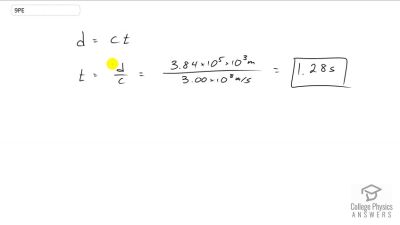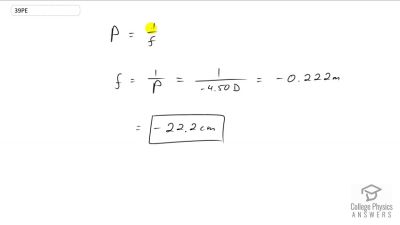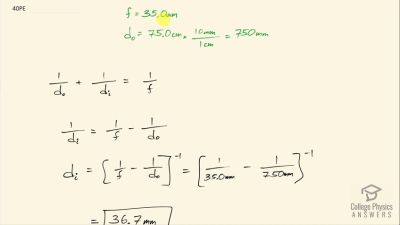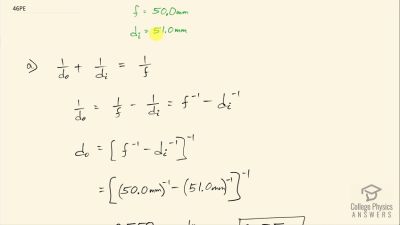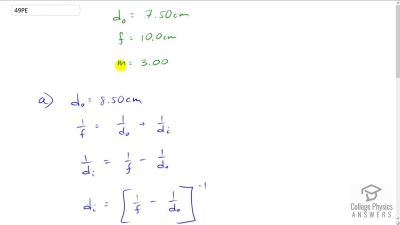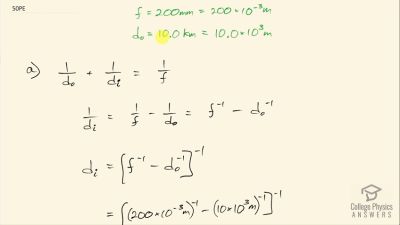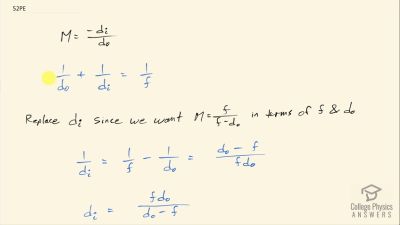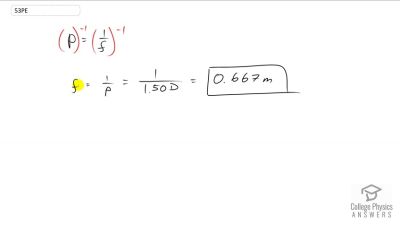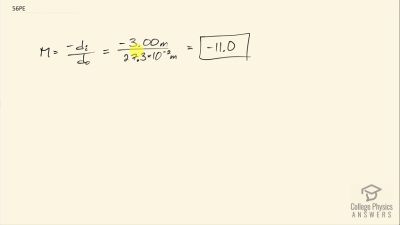Problem 1
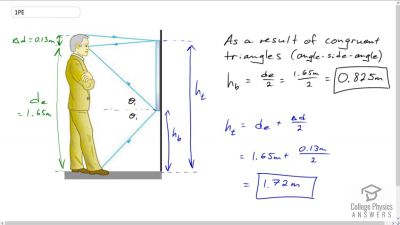
Suppose a man stands in front of a mirror as shown in Figure 25.49. His eyes are 1.65 m above the floor, and the top of his head is 0.13 m higher. Find the height above the floor of the top and bottom of the smallest mirror in which he can see both the top of his head and his feet. How is this distance related to the man’s height?