Question
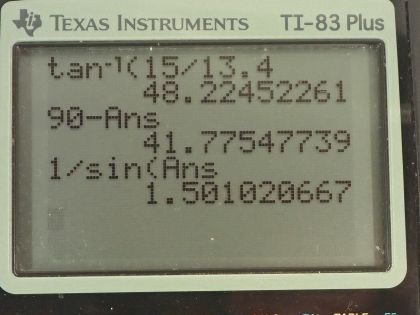
A ray of light, emitted beneath the surface of an unknown liquid with air above it, undergoes total internal reflection as shown in Figure 25.55. What is the index of refraction for the liquid and its likely identification?
Final Answer
. This is benzene.
Solution video
OpenStax College Physics for AP® Courses, Chapter 25, Problem 26 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
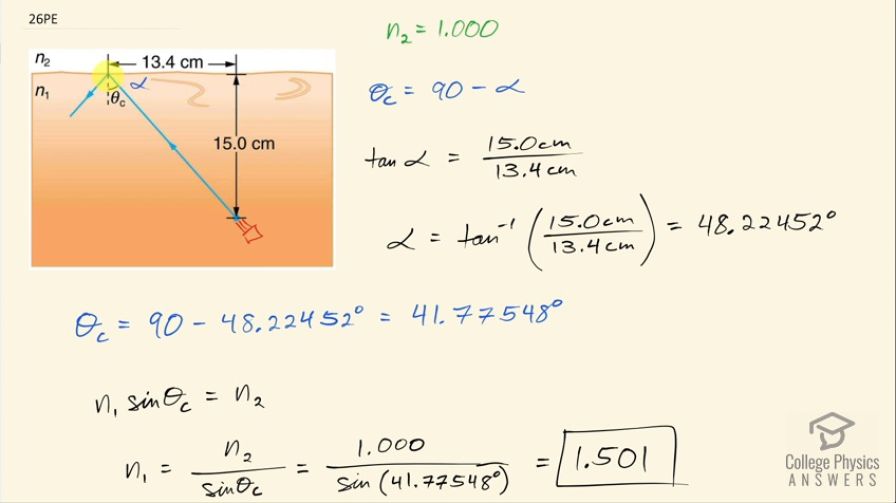
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Light is being emitted by some light source inside this liquid and light travels up and hits this interface between the liquid and air and then has total internal reflection and this is the smallest angle such that total internal reflection occurs and that makes it the critical angle. So we have to figure out what is the index of refraction of this material, what is n 1 in other words and then looking up in the table [25.1], we'll figure out what this material might be. So we can figure out what this angle α is using trigonometry based on the dimensions given to us here and then knowing that this dotted black line is a perpendicular to the interface, we can say that Θ c then is 90 minus this angle α that we'll find and then knowing the critical angle, we'll figure out what n 1 is. Okay! So the critical angle is 90 minus α so let's figure out α. The tangent of α is the opposite leg of this right triangle divided by the adjacent leg so that's the inverse tan then of 15.0 centimeters divided by 13.4 centimeters and that gives an angle of 48.22452 degrees, keeping lots of digits since this is an intermediate calculation. So I took the inverse tan of both sides here by the way to figure out α. Okay! So that's α and so then Θ c — the critical angle— is 90 minus that α and that works out to 41.77548 degrees. And then we use this formula with the critical angle and we have the first index of refraction the index of refraction of the first material that the light is traveling through which is this orange liquid multiplied by sin of whatever the critical angle is equals the index of refraction of the second medium, which is air in this case. So we solve for n 1 by dividing both sides by sin Θ c and then n 1 then is n 2 over sin Θ c. So that's 1.000 divided by sin of this angle that we found and this works out to 1.501. And when we look up in table [25.1], we look at liquids with an index of refraction of 1.501... we find it here and the material must be Benzene. So this liquid is Benzene.