Question
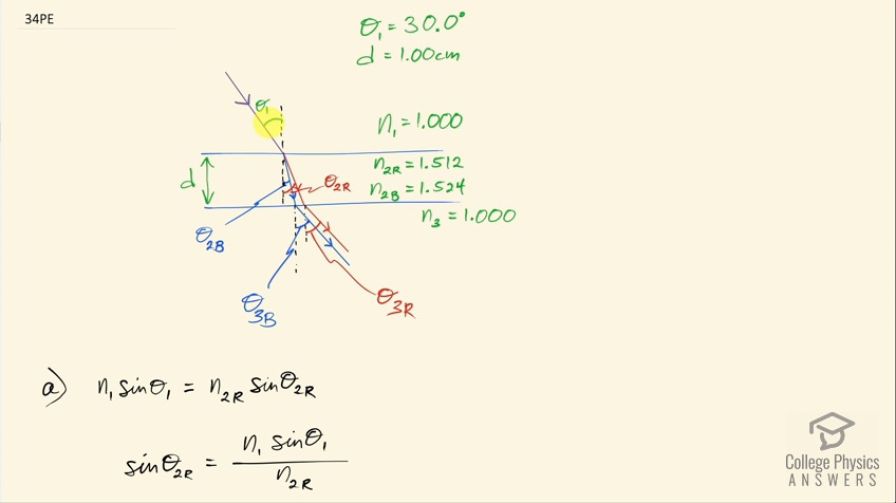
A narrow beam of light containing red (660 nm) and blue (470 nm) wavelengths travels from air through a 1.00 cm thick flat piece of crown glass and back to air again. The beam strikes at a incident angle. (a) At what angles do the two colors emerge? (b) By what distance are the red and blue separated when they emerge?
Final Answer
- Both colors emerge at
Solution video
OpenStax College Physics for AP® Courses, Chapter 25, Problem 34 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
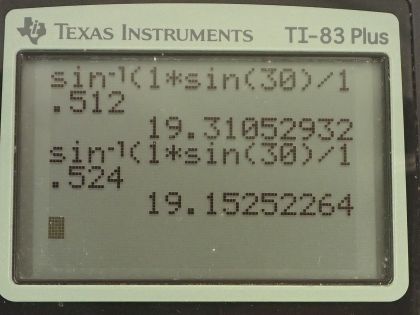
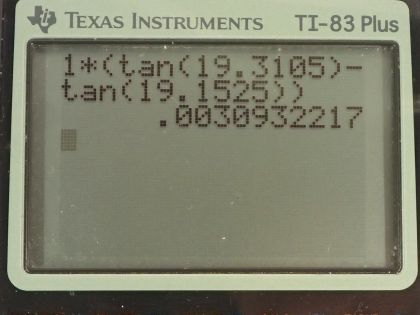
This is College Physics Answers with Shaun Dychko. A beam of light that consists of red mixed with blue which makes purple is incident at an angle of 30.0 degrees— that's Θ 1— on a piece of crown glass; initially, it's going through air which has an index of refraction of 1.000 for both the colors and then once it enters crown glass, each color has its own index of refraction so we look in table [25.2] to find the index of refraction in crown glass for red, which is 1.512 and blue, which is 1.524— so those numbers are recorded here— and then it enters into the air again which has an index of refraction again of 1.000 for both colors. So the blue will refract towards the normal more than the red because the blue sees the crown glass as having a higher index of refraction than red does and then the blue will exit the crown glass at this position and the red a little bit over here. Now the first question in part (a) is what will these angles be in the air after leaving the crown glass? So we want to find Θ 3 for blue and Θ 3 for R— 3 indicating the third medium. So the first medium is air, second medium is crown glass and then third medium is air again. So first let's figure out for red: we'll figure out Θ 2 for red in a crown glass and we apply Snell's law to this interface for red so that's n 1sin Θ 1 equals n 2R times sin Θ 2R; this n 1 and the Θ 1 do not get subscripts R or B later for blue because they are the same number for both colors. So sin Θ 2R then is n 1sin Θ 1 over n 2R because you can divide both sides here by the index of refraction for red in the crown glass— second medium— and then let's turn our attention to the second interface between material two and material three and apply Snell's law there so we have n 2Rsin Θ 2R equals n 3sin Θ 3R and sin Θ 3R after dividing both sides by n 3 is n 2Rsin Θ 2R over n 3 but sin Θ 2R, we have an expression for from here and we plug that in here. So we replace sin Θ 2R with n 1sin Θ 1 over n 2R and so this index of refraction of red and the crown glass cancels on top and bottom and we are left with the angle at which the red emerges in the third medium or in the air is n 1sin Θ 1 over n 3 but n 1 and n 3 are the same because they are both air and we can replace n 3 with n 1 then in which case it cancels and so we have sin Θ 3R is sin Θ 1 which means since the sin of these two angles are the same, the angles themselves must also be the same or you could say let's take the inverse sin of both sides and we have Θ 3R, on the left, equals 30.0 degrees on the right because that's what Θ 1 is. And we could do the same process for Θ 3 for the blue and we would arrive at the same answer: 30.0 degrees. In other words, this crown glass does nothing to change the direction of this beam of light for either color because it's returning back to the same medium that it started in, which is air. Okay! So this second interface kind of undoes whatever change in direction occurred at the first interface. Now one thing that is different though is the position at which these two colors emerge because they have different angles traveling through the crown glass and so we want to find out what is the difference between the distance that the red color is displaced compared to where it entered the crown glass versus the distance that the blue ray is displaced so x B and x R we are going to find and we want to figure out the difference between them. So we consider a right triangle here— we'll consider red first— and so we have this triangle here... this red line is a hypotenuse and then this opposite is what we want to find— that's gonna be x R— and then we have this adjacent here, which is the thickness of the crown glass which we are told is 1.00 centimeters and we can figure out what Θ 2R is and then using tangent, we can figure out what this opposite leg is x R. So the tan of Θ 2R then is x R divided by d— d being the thickness of the crown glass— and then we'll solve for x R by multiplying both sides by d so x R then is d times tan of Θ 2R. Now tan of Θ 2B is the same equation but with, you know, terms for the blue color inserted so we have x B divided by the same crown glass thickness, d and multiply both sides by d again and you have x B, the displacement of the blue through the crown glass is the thickness of the crown glass times tan of Θ 2B. So we can replace both terms here and here with these expressions and we have then the difference in the positions where the colors emerge from the crown glass is dtan Θ 2R minus dtan Θ 2B, we can factor out the d and we have d times tan Θ 2R minus tan Θ 2B. So we need to figure out what these angles are now and then plug in those numbers and then we'll figure out Δx. So the Snell's law at the first interface between the air and the crown glass for red is n 1sin Θ 1 equals n 2Rsin Θ 2R and we are actually going to plug in numbers this time and figure out what this angle is and we have kind of done this before already up here to figure out sin Θ 2R but we never did figure out the numbers. So we are dividing both sides by index of refraction for red in crown glass and we have sin Θ 2R is n 1sin Θ 1 over n 2R and then take the inverse sin of both sides and we have then the angle Θ 2R is the inverse sin of 1.000 times sin of 30.0 degrees— incident angle— divided by 1.512—index of refraction for the color red in crown glass— and this is 19.3105 degrees. So we have found this angle just now and then for blue, it's the same type of equation but with terms for the blue color and we have then that the angle two for the blue color is the inverse sin of 1.00 times sin 30.0 divided by— the index of refraction for blue in crown glass—1.524 and this gives an angle of 19.1525 degrees. So Δx then is 1.00 centimeter— thickness of the crown glass— times tan of 19.3105 degrees— this is the angle for red— minus tan of the angle for blue and this works out to 30.9 micrometers because our answer is going to be in centimeters since we multiplied this dimensionless number— this difference between these tangents is dimensionless— we multiplied it by centimeters and so we get 0.00309 centimeters and this works out to 30.9 micrometers.