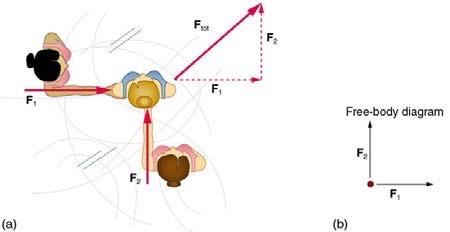
a)
b)
c)
Note: in some version of the textbook table 5.1 has a typo for the static friction of steel on ice. The static friction coefficient of 0.40 is incorrect. We expect a much lower coefficient for steel on ice since, from experience skating, the coefficient of static friction should be very small since it's really slippery standing on ice with skates on. 0.40 is a coefficient comparable to wood on wood (0.50), which is not slippery. Also, https://www.engineeringtoolbox.com/friction-coefficients-d_778.html gives a steel on ice static friction coefficient of 0.03, so I've presumed that the textbook author meant to write 0.04.
Solution video
OpenStax College Physics, Chapter 5, Problem 7 (Problems & Exercises)
Calculator Screenshots
Comments
On my table 5.1 Steele on ice for static friction is 0.40
Also, because she is initially stationary doesn't that mean she is not moving. Meaning that her acceleration would be zero?
Hi marievillafuerte, thanks for the question. It's possible there's a typo in your edition of the text. Perhaps you're using an older printed version? I'm seeing 0.04 in the pdf downloaded from https://openstax.org/details/books/college-physics-ap-courses. Also, we expect a much lower coefficient for steel on ice since, from experience skating, the coefficient of static friction should be very small since it's really slippery standing on ice with skates on. 0.40 is a coefficient comparable to wood on wood (0.50), which is not slippery. Also, https://www.engineeringtoolbox.com/friction-coefficients-d_778.html gives a steel on ice static friction coefficient of 0.03.
The skater moves as a result of being pushed by other skaters so, while she does begin from rest, she will be accelerated by the push from her two fellow skaters.
Hope that helps,
Shaun
0 is actually the answer, you are right.
Hi! i am also seeing that the text book provides a value of .4 rather than .04. I am using the most current edition of theOpenstax book found online.
Hi alexgoble, thanks for the comment. 0.04 is definitely the best estimate for the coefficient of static friction for steel on ice. Some editions of the OpenStax text list 0.40 in table 5.1, as you've noticed. I'm using revision number "CPFAC-2015-002(03/17)-BW", which is the latest high res. version of the College Physics for AP Courses. Perhaps the regular "College Physics" text not intended for AP courses has an outdated table? In any case, 0.40 is an error, which can be verified by considering other data sources such as https://www.engineeringtoolbox.com/friction-coefficients-d_778.html. Thanks again for mentioning it though, since getting feedback from students with sharp eyes helps make College Physics Answers the best resource it can be.
How did you know about the static friction being 0.04? it doesn't say it on the problem.
Hi Rafmaster333, thank you for that question. It's a question shared by a couple of other students as well, so please just look at my replies to them above your comment. The short answer is that the textbook is incorrect to say 0.4, whereas an internet search says 0.04 is reasonable.
Hey guys, I am also seeing the Static Friction of steel on ice for 0.4. Which would make part B) 0 for acceleration. The formula is correct but and works for part C) it is just the wrong static friction.
Hi trwatkins, thank you for noticing this discrepancy between the textbook and the solution. Other students have noticed this also. I have made a note below the final answer to explain that the figure in the textbook is a typo, and the static friction coefficient should be 0.04.
I'm confused about part b. The answer appears to be Zero acceleration whereas the solution was different. I was hoping for some clarification. Thanks!
Hi bjappell, thank you for the comment. There is a net force on the skater in part (b) since the total force exerted exceeds the friction force, so the acceleration is not zero. If you could expand on what isn't clear I might be able to help better.
All the best,
Shaun
What I don't get is how we can use static friction when there's an acceleration. An acceleration means there's motion, and that makes me think to use kinetic friction. What point in time is the problem referring to if there's both an acceleration of the skater and static friction? Is it the first moment when she starts to move or just before then, or is it some point in time that inexplicably covers both of those moments? I don't get it.
Hi rrincones, thank you for the question. In part (b), where the skater is initially at rest, in which case static friction applies, we're considering only the brief instant when they're just beginning to accelerate. It might be helpful to think of it as an instantaneous force, which admittedly is an idealization. In part (c) the skater is already sliding, so then kinetic friction applies.
Careful with the idea of moving = kinetic friction. It's more accurate to say sliding = kinetic friction. Car tires normally have static friction (sometimes call "rolling friction" since it's not strictly static), unless the car is sliding, in which case there would be kinetic friction.
Hope this helps,
Shaun
n
I keep plugging the same thing in my calculator to find the Angle and it gives me a totally different answer. 0.557?
Hello, thank you for the question. A typical reason for an issue like this would be having your calculator in radian mode, which means it gives the answer is radians instead of degrees. In radians, the answer would be 0.61377, that's still different than 0.577. My suspicion is that your calculator is in radian mode, and something is being typed in slightly different... it's hard to say. When you figure out the issue please let us know.
All the best,
Shaun





