Question
A wire is drawn through a die, stretching it to four times its original length. By what factor does its resistance increase?
Final Answer
Solution video
OpenStax College Physics, Chapter 20, Problem 35 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
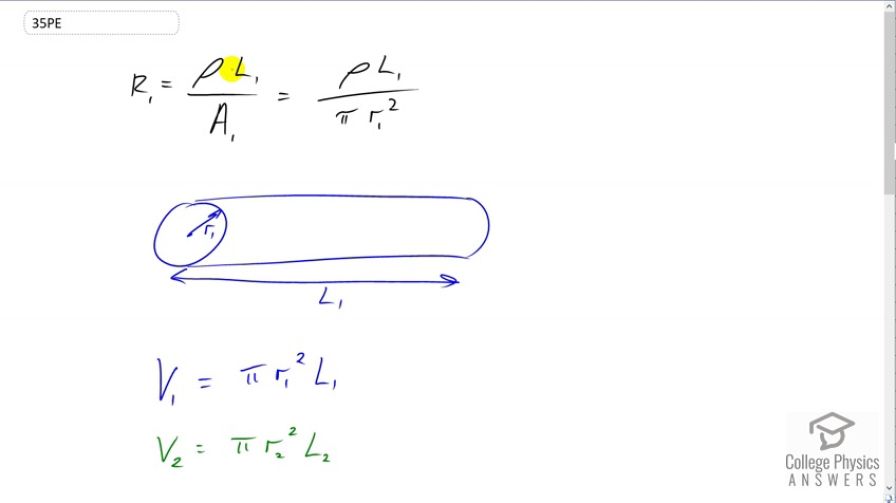
This is College Physics Answers with Shaun Dychko. We have a wire that is stretched to four times its original length and the question is by what factor does its resistance increase? We do expect the resistance to increase because the resistance is directly proportional to the length. So if length were to increase by four times you'd expect the resistance to increase by four times. But things are not quite that simple in this question because not only is the length increased but the way it's done is by keeping the same material putting it through a die which is a device that will squish the metal so that it becomes longer but in order to become longer it has to become thinner. So the cross-sectional area is also going to change as the length changes. Now the thing that will not change is, the volume of material will stay the same. So we're going to figure out what the new radius of our wire will be after the length increases by four times and then we'll be able to substitute for both of these factors here. Not only do we substitute for l one in calculating our new resistance, but we also need to figure out what should be substituted in place of the new radius. So the volume in the first case originally is pi times r one squared times l one, so this is the volume of a cylinder which we're going to model the wire as, is the cross-sectional area multiplied by its length. Then after it goes through the die and it's stretched out, it's going to have -- well I put a subscript on here for a new volume but then down here we say that the volumes are the same, so I don't really need o put a subscript on the V. But we do need a subscript on the radius and the length. So it's going to be pi times r two squared times l two. Now we're told that l two is four times l one. So we'll substitute that in for l two here and multiply it by r two squared and pi and then equate that to volume one because we're told that volume two and one are the same. So that's pi times r one squared times l one and then r two squared then after you divide both sides by four pi l one, this gives you r one squared over four. Then take the square root of both sides and you get r two is r one over two. So the radius of the wire after it's stretched is going to be half of what it was originally. So the resistance after it's been stretched, call it R two , is going to be the resistivity multiplied by the new length divided by pi times the new radius squared. We know that the new length is four times l one and then we've just figured out that the new radius will be half of what it was before, r one over two, and we square that. This makes a one over four in the denominator and so we multiply top and bottom by four. This works out to -- this two becomes squared there so this is really a four there, which cancels with this four and we're left with 16 on the top. So we have 16 rho l one over pi r onesquared. This is R one and so we have R two is 16 times R one. So the resistance has changed by a factor of 16.
Comments
this is wrong [professor said it will increase by a factor of 4

