Question
Hydroelectric generators (see Figure 20.43) at Hoover Dam produce a maximum current of at 250 kV. (a) What is the power output? (b) The water that powers the generators enters and leaves the system at low speed (thus its kinetic energy does not change) but loses 160 m in altitude. How many cubic meters per second are needed, assuming 85.0% efficiency?

Final Answer
a)
b)
Solution video
OpenStax College Physics, Chapter 20, Problem 63 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
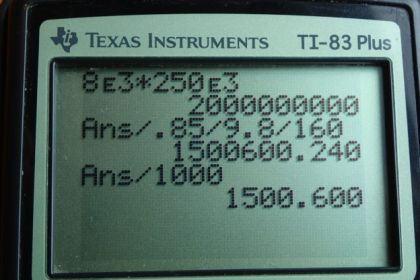
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The power output of the generators at Hoover Dam equal the current that is going through them multiplied by their voltage. And the current is eight times ten to the three Amps and the voltage is 250 kilo Volts which we convert into just regular volts by multiplying by ten to the three, so prefix kilo means ten to the three, so in 250 times ten to the three Amps and that makes 2.0 Giga Watts. And Giga is the prefix for ten to the power of nine. And then, whereas what is the rate of volume of water going through the dam, in cubic meters per second? So, we assume that there is an 85 percent efficiency in energy conversion and that is the gravitational potential energy of the water is being converted into electrical energy. And that conversion is happening at a rate of 0.85 which is 85 percent. And so, we have the power output of the generators is 0.85 multiplied by the power input, so to speak of the falling water. And the power input is going to be the potential energy change of the water divided by time. And the potential energy will mg times the height through which it falls and that’s divided by time. And so we substitute this in place of P in. Let me write that in red here. And, we are going to solve this m over t because this will give the volume rate of flow of-- or the mass rate of flow, I should say, of the water. And then we’ll convert this kilograms per second into meters cube per second in our last step here, by multiplying by the-- or dividing by the density. So, m over t, well, we get that by multiplying both sides by one over 0.85gh. And that gives us m over t is power output over 0.85 gh. The power output we know is two Giga Watts or two times ten to the nine Watts. And we divide that by 0.85 times 9.8 meters per second squared times 160 meters is we are told that’s the height over which the water falls. And that gives 1.5006 times ten to the six kilograms per second. And you could confirm that these are the units by turning watts into its base units and then see that things cancel with the units that are in the bottom and leaving kilograms per second behind. And remember that watts is joules per second and then-- joules are, well, you know you get your work by force times distance. So the joules come from newtons multiplied by meters. And then, newtons is well, force equals ma. And so the newtons comes from units of kilogram times meter per second squared. And so one thing leads to another and you’ll end up with kilograms per second. Then, multiply that by one cubic meter for every 1000 kilograms of water. So this is the-- we’re dividing by the density or multiplying by the reciprocal of the density of water. And assuming it’s out of boat 15 degrees Celsius. And that gives 1.5 ten to the three cubic meter per second.