Question
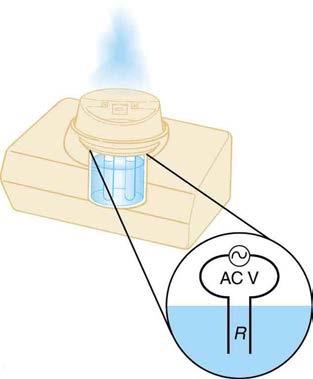
Cold vaporizers pass a current through water, evaporating it with only a small increase in temperature. One such home device is rated at 3.50 A and utilizes 120 V AC with 95.0% efficiency. (a) What is the vaporization rate in grams per minute? (b) How much water must you put into the vaporizer for 8.00 h of overnight operation? (See Figure 20.42.)
Final Answer
a)
b)
Solution video
OpenStax College Physics, Chapter 20, Problem 59 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
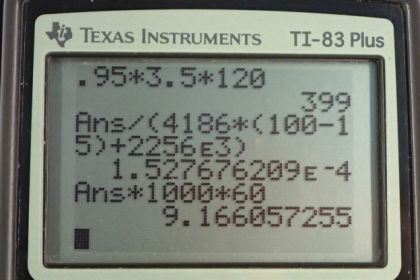
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The current that the vaporizer passes through the water is three and a half amps at a voltage of 120 volts and the efficiency is 95 percent which means that 95 percent of the power output of the vaporizer goes into the water, energy going into the water to make it vaporize. So the rate at which energy is going into the water, the power output, is the efficiency times the power consumed or input into the system. So that's 0.95 multiplied by I V, and that is 0.95 times three and a half amps times 120 volts which gives 399 watts. So 399 watts is the rate at which energy is going into the water. Now the amount of energy needed to make water vaporize is the energy needed to increase its temperature to 100 degrees plus the latent heat of vaporization. So this term here is the amount of energy needed to do the phase transition from liquid to gas. We'll assume that the water is initially at say 15 degrees, did I say? Yeah, 15 degrees. So we can factor out the m, and it's going to be the specific heat of water times change in temperature plus the latent heat of vaporization. It's the mass per time that we're interested in and that's going to equal -- did I say mass per time? I mean energy per time that we're interested in here and that is the same units as power output here. Power output is joules per second so here we have joules of -- in, I don't know why it's the letter Q, but it's joules per time here as well. Okay. So we'll substitute for Q as m c delta t plus l V over -- and that's over t equals P out. We'll divide both sides by this binomial here and we get the mass per time because we're interested in grams per minute that this vaporizer outputs. So we have mass per time equals the power output divided by the energy needed to vaporize some water. So we have 399 watts divided by the specific heat of water which I looked up in table 14.1, that's chapter 14, 4186 joules per kilogram per Celsius degree, times the change in temperature and we'll assume it starts at 15 degrees Celsius, that's 100 degrees Celsius boiling point minus 15. Then we'll add to that the latent heat of vaporization of water which is in table 14.2 which is 2256 times ten to the three joules per kilogram. All this works out to 1.5277 times ten to the minus four kilograms per second. Now we want our units to be in grams per minute so we multiply by 1000 grams per kilogram and then multiply by 60 seconds per minute and we're left with grams per minute. This is 9.17 grams per minute. Now the number of liters of water that we have to add to the vaporizer so it can operate for eight hours all night, will be this rate of vaporization, grams per minute and then we have to do a bunch of unit conversion to turn this into liters given an eight hour run time. So we multiply by eight hours but that's no good because we have minutes on the bottom there and that doesn't cancel with hours so we have to multiply by 60 minutes per hour. So now we're all good with the time units and then we convert the grams -- well, we'll convert the grams into kilograms so that we can multiply by this density of water that I looked up using a search engine. So we have one kilogram for every 1000 grams giving us kilograms now, and then multiply by one cubic meter of volume for every 999 kilograms. This is the density at 15 degrees Celsius. Now we need to convert this cubic meters into liters by multiplying by 1000 liters for every cubic meter. Now finally, we have liters. So that's 4.40 liters of water should be added to the vaporizer at a minimum so that it operate for eight hours all night.