Question
Find the time after when the instantaneous voltage of 60-Hz AC first reaches the following values: (a) (b) (c) 0.
Final Answer
Solution video
OpenStax College Physics, Chapter 20, Problem 83 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
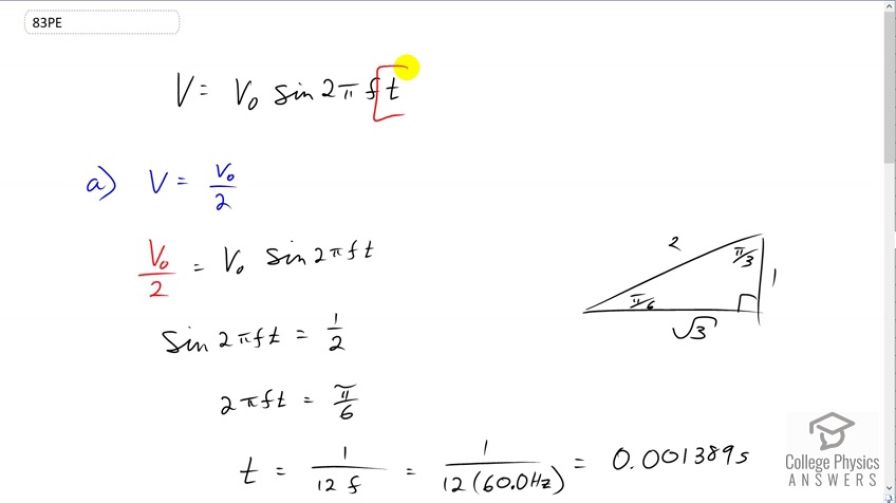
This is College Physics Answers with Shaun Dychko. The voltage of an AC circuit is the peak voltage multiplied by sine of two pi times its frequency, multiplied by the time. You know, this is meant to give you the voltage as a function of time. So we're asked to find out what is the time at which the voltage will be half of its peak. So we substitute V naught over two in place of V. Then divide both sides by V naught and this gives us one half equals sine of two pi ft. One half, we can figure out what this is, this argument for the sine function by considering this special triangle. Because if we have a triangle with angles of pi over three which is 60 degrees and pi over six which is 30 degrees, we have these side lengths of one opposite the pi over six angle, two is the hypotenuse and root three is opposite the pi over three angle. So if we have one over two, it's the sine of pi over six is one over two. So that means we know that this thing that we're taking the sine of, two pi ft has to be pi over six. You could also use your calculator and make sure that it is in radian mode. You can take the inverse sine of a half and it would give you whatever pi over six is as a decimal. Then we solve for t by dividing both sides by two pi f and so we get t is one over 12 times f. The pi's cancel on both sides here, and the six times two make the 12 there. So we have one over 12 times 60 Hertz which is 1.39 milliseconds. So assuming that it -- the question is at what time after t equals zero will the voltage be half of the peak? The answer is after 1.39 milliseconds. Then the question is, after how much time will the voltage equal the peak? So we substitute V naught in place of V. Well, divide both sides by V naught and you get sine of two pi ft equals one. Again, you could use your calculator in radian mode and take the inverse sine of that that we find, but I prefer to get exact answers. I'm going to use this unit circle which is used to define cosine and sine. Cosine and sine are not defined in terms of triangles. I mean when you're first introduced to trigonometry that's how they're explained but triangles can't have an angle more than 90 or well, you can't have big angles in a triangle. You can't have an angle that's more than 180 degrees in a triangle so in order to -- but you can take the sine or the cosine of an angle more than 180 degrees. So for large angles you need a different definition for cosine and sine. Anyway this is a whole topic in math that, you know, we could have a whole lesson on. But just try to not take this too long here. So we have this unit circle, the x coordinate of a point on the circle is cosine of whatever the angle is and the y coordinate is the sine of the angle. So the number one is here and so it has a cosine of -- well, cosine of pi over two is one. We don't actually care about that. What we care about is that the sine -- sorry I didn't say that right, the cosine of pi over two is zero by the way. But it's the y coordinate that is the sine of this angle. So the y coordinate at this point is one and so the sine of pi over two makes one. So it's coordinates zero, one. So, I hope I haven't lost you there but yeah. We have this whole thing must be pi over two because the sine of pi over two is one, the y coordinate of a point on the unit circle. Then we will divide both sides by two pi f and we get the time is one over four times frequency. So one over four times 60 Hertz and that is 4.17 milliseconds. Then when will the voltage be zero? So we substitute zero in for V and that means this whole thing must be zero. Well, the sine of what makes zero? The sine of pi makes zero because this point here has a y coordinate of zero. So the y coordinate here is a second coordinate, and so what angle makes this point here positioned there? The angle pi does and so the sine of pi is what makes zero. So we write pi there and then we divide both sides by two pi f and then the time is one over two f. So, one over two times 60 Hertz which is 8.33 milliseconds.
