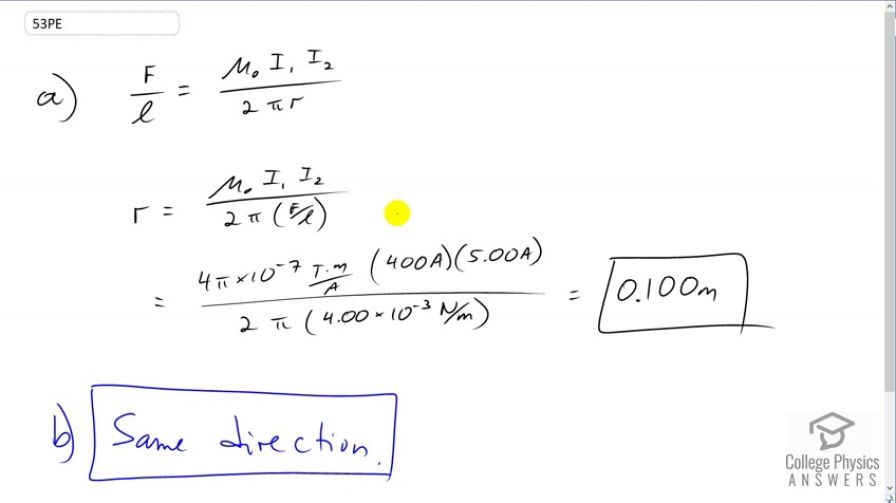
The wire carrying 400 A to the motor of a commuter train feels an attractive force of $4.00\times 10^{-3}\text{ N/m}$ due to a parallel wire carrying 5.00 A to a headlight. (a) How far apart are the wires? (b) Are the currents in the same direction?

Video Transcript

This is College Physics Answers with Shaun Dychko. One of the wires carrying 400 Amps to the motor of a commuter train is running parallel to a wire carrying only 5 Amps to the headlights. And we’re told that the attractive force is, between them, force per length, and that is four times ten to the minus three newtons per meter. And so we’re gonna solve for r by multiplying both sides by r and this force per length. Normally I don’t have fractions within fractions but I’m going to do that this time because this is a single number that we’ve been provided by the question, this ratio, so I’ll treat it as a single thing. So on the left we’ll have r, and on the right we’ll have all of this with F over l in the denominator. So we have permeability of free space times the first current times the second current divided by two pi times four times ten to the minus three newtons per meter, and that gives us 0.100 meters. That’s the separation between the wires. And because this force is attractive, the current must be going in the same direction.