Question
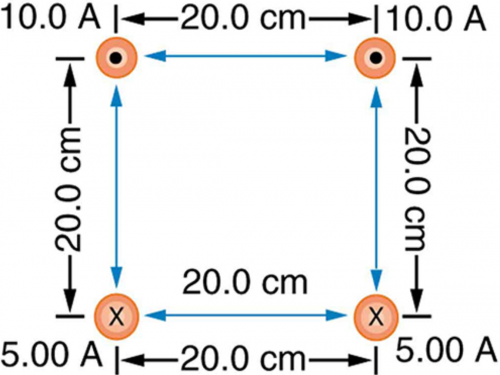
Find the magnitude and direction of the magnetic field at the point equidistant from the wires in Figure 22.58(b), using the rules of vector addition to sum the contributions from each wire.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 22, Problem 70 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Using vector addition, we are going to find the net magnetic field at the point that is equidistant from each of these four wires, which is the center of the square. So wire number one produces a magnetic field that is up into the right and it has a line that is long— it's twice as long as the line due to the magnetic field of wire four— and both of these wires produce magnetic fields up into the right and you can verify it by... with number four for instance putting your thumb in the direction of the current which is into the page and then position your fingers at the center of the square and you will find that they are pointing up into the right. Likewise with this top left corner wire if your thumb comes out of the page, your fingers in the middle of the square are pointing up into the right. Now the current in wire one is 10.0 amps whereas it's only 5.00 amps in wire four and so that makes the magnetic field twice as big and so the vector is meant to be twice as long here because the distances are the same. Okay! And then we have wire two and wire three both producing magnetic fields that are down into the right and magnetic field due to wire two is of the same length as the magnetic field due to wire one because it has the same current 10.0 amps and wire three produces a magnetic field due to this 5.00 amp current and so this shorter length is the same as B 4. So the magnitude of the magnetic fields due to wires one and two is μ naught times current one or current two divided by 2π times the distance between the wire and this central point which is r with no subscript because it's the same r for all of the different wires and we found r by taking the square root of half this side length, which is 10.0 centimeters or 20.0 divided by 2 and then we square that and add that to half this vertical side length so this is a right triangle, which is 10 by 10 and we are using the Pythagoras here to find the length of the hypotenuse and that's gonna work out to 14.1421 centimeters. Okay! So the y-component of the magnetic field due to wire one is equal in magnitude and opposite in direction to the y-component due to magnetic field from wire two. So this would be... this little portion here would be B 1 y-component and then over here will be B 2 y-component and they are of equal magnitude because you have the same angle here— this angle Θ is 45 degrees— because we have a... when you have a diagonal of a square and then you have the other diagonal of a square, they are gonna intersect at 90 degrees here and then this is halfway bisecting that angle and so that makes Θ 45 degrees. And so these y-components are gonna cancel and we can just say that based on the symmetry of this problem and the y-components due to magnetic fields from wire three and four are likewise going to cancel and so the total y-component of a resultant here is zero. We also have a formula here for the magnitude of the field due to wires three and four: it's μ naught times I 3 over 2πr and the only calculation we are gonna have to do then to find the resultant is to find the x-components of each of these vectors and they are all pointing to the right and so we just add them all together. So we have the x-component of magnetic field due to wire one, two, three and four all added together and so we take the magnetic field of each wire and multiply it by cosine of 45 because it's the adjacent leg of each of the triangles that we are concerned with and then we substitute for B 1, B 2, B 3 and B 4 here; it's not a typo to put number three there because the current in wire four is the same as the current in wire three and likewise the current in wire two is the same the current in wire one— two and one are both 10.0 amps; three and four are both 5.00 amps— and then we factor out common factors— μ naught times cos 45 over 2πr— from each of these terms and you have 2I 1's plus 2I 3's but I 3 is half of I 1 because 5.00 is half of 10.0 and so we can substitute that in in which case we have 2 divided by 2 is 1 so that's 3I 1 over 2πr and then multiply by μ naught times cos 45. So we have 3 times 4π times 10 to the minus 7 tesla meters per amp times 10.0 amps times cos 45 over 2π times 14.1421 times 10 to the minus 2 meters and that gives 3.00 times 10 to the minus 5 tesla to the right is the resultant magnetic field.
