Question
A mass spectrometer is being used to separate common oxygen-16 from the much rarer oxygen-18, taken from a sample of old glacial ice. (The relative abundance of these oxygen isotopes is related to climatic temperature at the time the ice was deposited.) The ratio of the masses of these two
ions is 16 to 18, the mass of oxygen-16 is , and they are singly charged and travel at in a 1.20-T magnetic field. What is the separation between their paths when they hit a target after traversing a semicircle?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 22, Problem 20 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
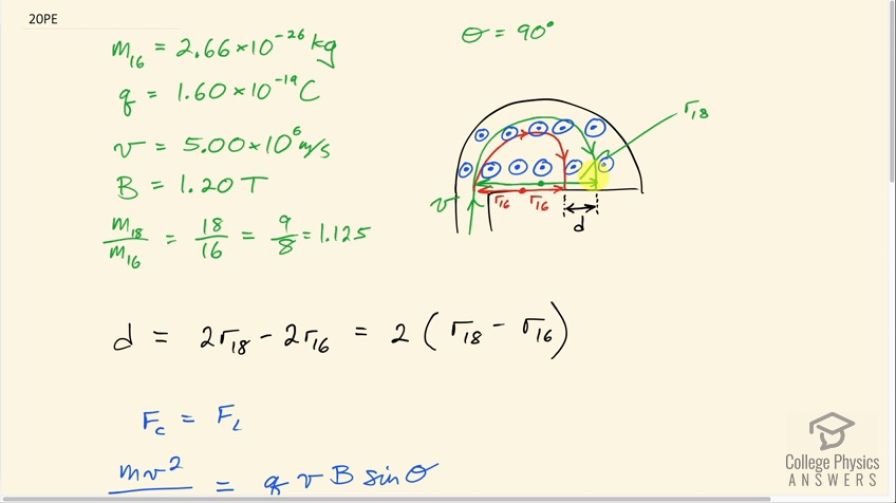
This is College Physics Answers with Shaun Dychko. A mixture of two oxygen isotopes from ice core samples are fed into this mass spectrometer and it consists of isotopes 16 and 18 and they are both going to have the same speed entering this semi-circular region that has a magnetic field pointing out towards us and they are going to have different radii though of curvature in this mass spectrometer because of their differing masses. And we can see that the lighter isotope-16 is going to have a smaller radius of curvature because it's not as heavy and so the same force is applied to it as is applied to the other isotope because they are going at the same speed in the same magnetic field with the same charge and so that force will result in a larger acceleration centripetal acceleration for the less massive isotope. Okay! So we want to find this distance d here, this separation between where the isotopes hit this... basically, there's a sensor here to tell you where the isotopes are hitting and they are hitting in various locations for different masses and you get a spectrum of positions and that's why it's called a mass spectrometer because the different positions on the spectrum indicate different masses. Okay! Now this case has only two places where particles are going to impinge on the sensor because there are only two isotopes involved. We are told that the mass of the isotope 16 is 2.66 times 10 to the minus 26 kilograms and they are singly charged, which means they have the elementary charge of 1.60 times 10 to the minus 19 coulombs. They are going at a speed of 5.00 times 10 to the 6 meters per second and in this section of the mass spectrometer, it's not drawn here or even mentioned in the question but there's a velocity selector where you have crossed electric and magnetic fields through which only particles with a certain velocity can travel straight. Okay! So they are all going at this speed and the magnetic field is 1.20 tesla and we are told that the ratio of masses of the two isotopes is 18 to 16, which is 1.125. So from this, we can figure out the mass of the isotope 18 so it's 1.125 multiplied by the mass of the 16 isotope. Alright! So this separation in terms of the radii because we can find the radii using some formulas that we have... we need to express this distance between where they hit the sensor in terms of the radii. So it's going to be this distance here from this starting position to this final position minus or taken away from this distance here and these highlighted distances are the diameters of these paths and so the diameter for the isotope 18 is 2 times r 18 and from that we are gonna take away the diameter of the radius or the diameter of the path for the isotope 16, which is 2 times its radius and they can factor out the 2 and we get this expression for d. Alright! Now let's find the radii: first, we'll say that the centripetal force is equal to the Lorentz Force so the centripetal force for any particle going in a circle is mass times speed squared over radius— that is any particle going at constant speed of course— and so mv squared over r is going to equal the Lorentz Force, which is the amount of charge multiplied by the particle's speed times the magnetic field strength multiplied by sin of the angle between the velocity and the magnetic field. In this case, the magnetic field and velocity are perpendicular because if you took a side view here, you would see these magnetic field lines pointing up so we take a view with your eyeballs here... you would see the fields pointing up and you would see the velocity going to the right and they are perpendicular. Okay! So we want to solve this for r: we multiply both sides by r over qvBsin Θ and then we say that r then is mass times speed divided by charge times magnetic field strength times sin Θ. So for oxygen 18, the radius then is m 18 whatever the mass of a single atom of oxygen 18 is multiplied by speed over qBsin Θ and the v, q and the B do not get subscripts here because they are the same for both isotopes; they are both going at the same speed, they have the same charge in the presence of the same magnetic field so the only thing that gets a subscript is the mass and mass 18 is 1.125 times mass 16 so we substitute that in here and the radius for the oxygen 16 is m 16v over qBsin Θ. So we substitute these two things in place of the radii terms in this formula for the distance between where the particles hit the sensor— this d does not stand for 'diameter' by the way. Okay! So we have made those substitution's here and we have a lot of common factors so we factored them all out and we are left with 1.125 from this term minus 1 from this term and we end up with 2 times the speed— 5.00 times 10 to the 6 meters per second— times the mass of an oxygen 16 atom, which is 2.66 times 10 to the minus 26 kilograms times 0.125, which is the difference between 1.125 and 1 divided by the charge—that's coulombs— times 1.20 tesla times sin of 90 and we end up with 17.3 centimeters is the distance we were trying to find.
