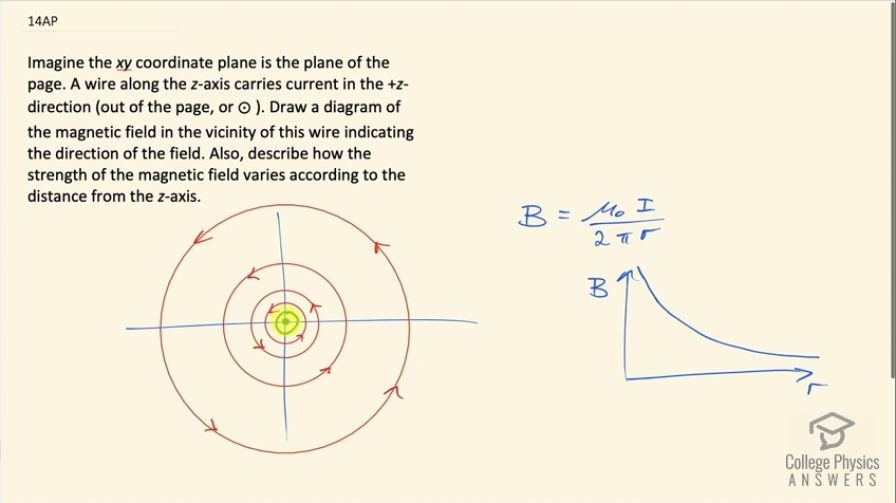
Imagine the xy coordinate plane is the plane of the page. A wire along the z-axis carries current in the +z-direction (out of the page, or ⊙ ). Draw a diagram of the magnetic field in the vicinity of this wire indicating the direction of the field. Also, describe how the strength of the magnetic field varies according to the distance from the z-axis.

Video Transcript

This is College Physics Answers with Shaun Dychko. A wire is carrying a current out of the page represented by a dot, which is like the point of an arrow coming towards us and the direction of the magnetic field around this wire is given by the right hand rule where you put your thumb in the direction of the current coming out of the page and you grasp the wire and the direction of your fingers is the direction of the magnetic field around the wire. So we have concentric circles that are centered on the wire and the spacing between the circles increases with distance and that represents the way in which the field strength is decreasing with distance the magnetic field due to current carrying wire is permeability of free space times the current divided by 2π times the distance from the wire and this is a reciprocal graph and so we expect the distance between these lines because each line represents the same magnitude decrease in magnetic field strength and so in order for differences in magnetic field to be the same between consecutive circles, the distance has to be greater the further away you get because if you look at this graph here and suppose the magnetic field lines are separated by this much magnetic field strength ΔB that represents this difference in ΔR and I will call this ΔR 1 because that's the first difference in radius. And then we have the same ΔB again going to here say and so the ΔB does not get a subscript because it's the same difference in magnetic field strength basically I am trying to draw the same the same vertical distance between amounts here but the amount of change in distance will be significantly more so this is ΔR 2 and you go the same amount of change in magnetic field down again and let's pretend that we are not hitting the axis here the difference in ΔR will be massive because this is asymptotically approaching the x-axis but never quite does and the difference in distance will be massive you have to go way over here before you get to the magnetic field low enough to make the same difference. Okay! Anyway... there we go!