Question
(a) Triply charged uranium-235 and uranium-238 ions are being separated in a mass spectrometer. (The much rarer uranium-235 is used as reactor fuel.) The masses of the ions are and , respectively, and the travel at in a field. What is the separation between their paths when they hit a target after traversing a semicircle? (b) Discuss whether this distance between their paths seems to be big enough to be practical in the separation of uranium-235 from uranium-238.
Final Answer
- Yes, this distance is big enough since one could harvest the different isotopes when they are separated by .
Solution video
OpenStax College Physics for AP® Courses, Chapter 22, Problem 21 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
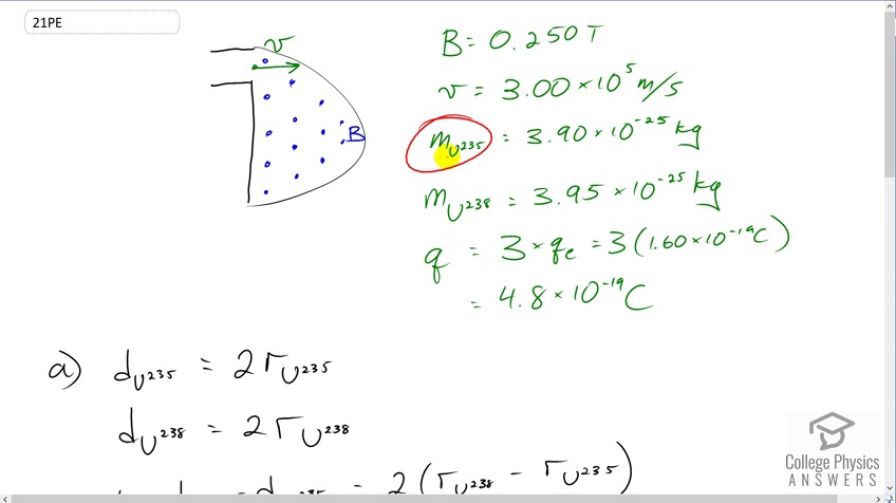
This is College Physics Answers with Shaun Dychko. We have a mass spectrometer here that's going to enrich the Uranium by putting more of the Uranium 235 isotope in the mixture. And it's going to separate these two isotopes because the Uranium 238 is going to have a different radius in its path through this portion of the mass spectrometer. Then, it will end up here whereas Uranium 235 being less massive will end up travelling a smaller radius path and it will end up here. So it's the 235 that's here closer to the entrance and then this is Uranium 238. Now, this entrance here to this portion where there's a magnetic field here, this is a velocity selector before that entrance. And so every charge particle entering this D-shaped area is going to be going at the same speed. And it talks about velocity selector somewhere else in here, textbook but a quick idea is that there's an electric field and a magnetic field in here both of which exert a force but in opposite directions on the charge particle in here such as that only ones with a certain velocity will go straight through. So, we have a bunch of data given to us and we're asked to find out what is this separation between where the Uranium 238 hits the target here and the separation between the Uranium 235 with the 238. So this distance here is delta d. So, there's a magnetic field strength 0.25 Tesla. The velocity of the particles entering are at three times ten to the five meters per second. Uranium 235 has this mass and Uranium 235 is slightly heavier by 0.5 kilograms times ten to the minus 25. And they're triply charged which means they have a charge of three times the elementary charge. So that's three times 1.6 times ten to the minus 19 Coulombs which is 4.8 times ten to the minus 19 Coulombs. So the total distance between the entry and where one of the isotopes lands is going to be two times the radius of its circular path. So if this is the radius of the Uranium 238, it's going to start here and then end up down here. Let's say 235 and it will end up down here. And this arrow is the radius and this total distance from where it hits the target and where it entered is going to be two radii. And the separation between where the two isotopes hit the target is going to be the difference between this distances or diameters in other words. And so that is two times the difference and the radii of the circular path. So, the centripetal force that the charge particular experiences is going to be provided by the magnetic force which is the charge times velocity times magnetic field strength, velocity and magnetic field being perpendicular here. And we can solve for r by multiplying both sides by r over qvB. And so there is the radius. Now, the separation between where they hit the target then is going to be two times the difference in the radii. So in the first case for Uranium 238, that's going to be the mass of that isotope times its speed divided by its charge times the magnetic field strength and then minus the radius for the Uranium 235 isotope which is going to be the same as for 238 but just with the different mass substituted. And so the speed and the charge and the magnetic field do not get subscripts because they are the same for both isotopes. So we can factor those common factors out. And we get that the distance between them will be two v over qb times the differences in masses. So that's two times three times ten to the five meters per second speed divided by 4.8 times ten to the minus 19 Coulombs times 0.25 Tesla times 3.95 times ten to the minus 25 kilograms minus 3.90 times ten to the minus 25 kilograms which is two and a half centimeters. And that is big enough distance to separate them because you can have a tiny, tiny scoop that would scoop up one pile here and then the other pile being two and half centimeters away is far enough that you can scoop one and not the other. So yes these isotopes can be separated.
