Question
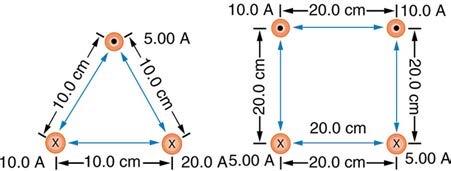
Find the direction and magnitude of the force that each wire experiences in Figure 22.64(b), using vector addition.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 22, Problem 57 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
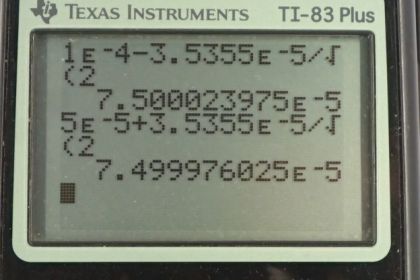
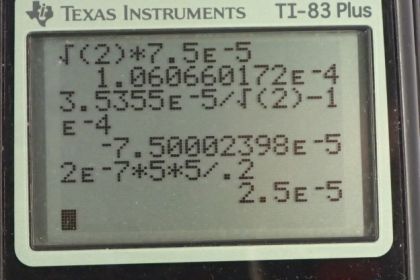
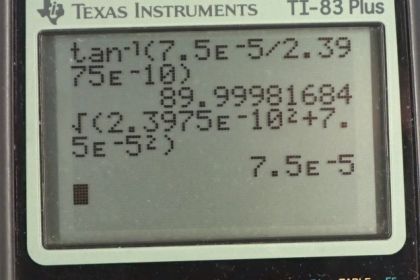
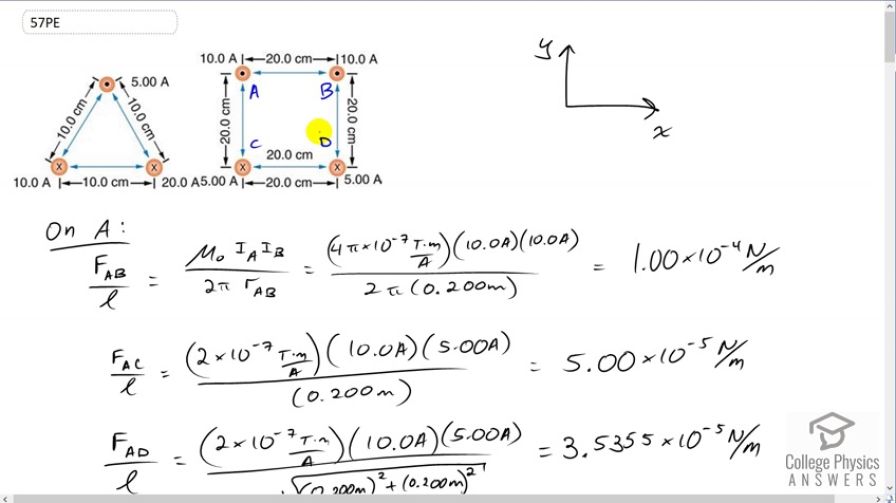
This is College Physics Answers with Shaun Dychko. We are going to calculate the force per length on each of these wires on the corners of the square. This square has side lengths of 20 centimeters and we’ll label this wire up here on the top left letter A, and this wire B, and we have C and we have D. And wires A and B carry a current of ten Amps out of the page towards you, and wires C and D have a current of five Amps going into the page. So the force per length between two wires is the product of the currents of the two wires times the permeability of free space divided by two pi times the distance between the wires. And so this line here is the force per length on wire A due to wire B. So we have currents A and B here and this r subscript AB is the distance between wires A and B. So we have 4 pi times ten to the minus seven Tesla meters per Amp, permeability of free space, times ten Amps in wire A times ten Amps in wire B, divided by 2 pi times the 0.2 meters between them. And that is one times ten to the minus four newtons per meter. Then we’ll find the force on wire A due to wire C per unit length, and I’m going to multiply by two times ten to the minus seven, and I’m going to do that from now on. This is a simplification of this, 4 pi times ten to the minus seven divided by 2 pi, is something that appears in our formula every time and so 4 pi divided by 2 pi is two, and still times ten to the minus seven. So multiply by ten Amps in wire A and then by five Amps in wire C, and divide by 0.2 meters and that gives five times ten to the minus five newtons per meter. And then we have the force on wire A due to wire D, and the distance between them, we have to get using Pythagoras, so it’s the square root of the sum of the squares of the two legs of this triangle here. So we have square root of 0.2 meters squared plus 0.2 meters squared, that’s the distance between wire A and the opposite corner wire D. So we have the product of the two currents in the wire times this constant divided by the distance, and that gives 3.5355 times ten to the minus five newtons per meter. So we have here a picture of all three vectors, all three forces per length that are acting on wire A. And we have the force on wire A due to wire B is attractive and so the force on wire A is to the right due to wire B. And the force on wire A due to wire C is repulsive because the currents are in the opposite direction, and so this is going to be a force upwards, which I’ve drawn here. And then likewise, the force on A due to wire D is also repulsive because they are of opposite direction currents, and so it’s going to be along this line here, and that’s at 45 degrees because this is a square and a diagonal and a square has an angle of 45. So to find the total x component on wire A, this is force on A per length, we take the force on A due to B because that’s entirely in the x direction, and that’s in the positive direction because we’re taking up to be positive and right to be positive. And then minus from that the component of the force on A due to wire D that is in the x direction, and that’s the force per length multiplied by sine of 45, so this is the opposite leg of this triangle here, and we get that by multiplying the hypotenuse by sin 45. Now sin 45 is, 45 is a special angle and here is a triangle for it. If you have a triangle with two 45 degrees angle, you’ll have side lengths one, one and the hypotenuse would be root two. And so sin 45 is the opposite divided by the hypotenuse, so one over root two. So I just prefer to write that in instead of putting sin 45 into my calculator, although you could sin 45 in your calculator and that would be fine. So we plug in numbers now. So that’s one times ten to the minus four newtons per meter, force on wire A due to wire B, minus 3.5355 times ten to the minus five newtons per meter, force per length on A due to wire D, times by sin 45 which is one over root two. Now we get 7.5 times ten to the minus five newtons per meter. That’s the total force in the x direction and it’s positive and so it’s to the right. And the force on a per length in the y direction is going to be the force on A due to C, which is entirely in the y direction, positive upwards, and then the component of the force on A due to wire D that is upwards, and so it’s also positive and so these are going to add together. And cos 45 also is one over root two. So we end up with five times ten to the minus five plus 3.5355 times ten to the minus five times one over root two, giving us this number here which is the same as the total force per length in the x direction, and that’s a bit of a coincidence. Now to get the angle of this force, we take the inverse tangent of the y component divided by the x component, and since they are the same, this is the inverse tangent of one which again is part of this special triangle. Inverse tangent of one is 45 degrees because a tan of 45 gives one. And so we have 45 degrees above the positive x axis, and we know that’s the case because our x component, well let’s draw those two. Our x component is 7.5 to the right because it’s positive, and our y component is 7.5 vertical, and so this resultant is going to have an angle that’s above the positive x axis. And then, we want to know what is the magnitude of this force per length. I keep forgetting to write in the per length here but I think you get the idea. So the magnitude of the force per length on A is going to be the square root of the sum of the squares of the x and y components on it, but since the x and y components are the same, we can say two times one of them squared, and the square root of one of them squared is just the thing, so FAx over l, and then times by square root two. You didn’t need to do any of this if you don’t like, you could just take the square root of one number squared plus that same number again squared and that would be fine, but I’m gonna go root two times 7.5 times ten to the minus five which gives 1.06 times ten to the minus four newtons per meter. And so we have this force per meter, 45 degrees above the positive x axis. And there is the force per length on wire A. Then, on wire B, we want to know the force per length on wire B due to wire A, and it’s going to be in the opposite direction to the force on A due to B which we’ve already found, and so it’s going to be negative 1.0 times ten to the minus four, so it’s this force here but in the other direction, it’s going to be to the left on wire B. And the force per length on wire B due to wire C, is going to be the same as the size of the force on A due to D, because C and D have the same currents so both five Amps and they are the same distances from each other. Wire C is the same distance from B as wire A is from D because they are on diagonals across the square so distance from C to B is the same as the distance from A to D. So where was I, here. So that means the force is the same magnitude, 3.5355 times ten to the minus five newtons per meter but now it’s going to be 45 degrees above the positive x axis, so it’s up and to the right. And the force on B due to wire D is the same as the force on A due to wire C, so the force on this one due to this is the same as the force on this one due to this, because they are equal separation and equal currents involved. And that is five times ten to the minus five newtons per meter. And so here are all the different forces on wire B, we have a repulsion from the opposite corner wire C, we have a repulsion from wire D and we have an attraction to wire A. Now the total x component force per length is going to be the force per length due to wire C which is on the diagonal so we’re taking cos 45 to get the component of that force in the x direction and that’s going to be positive to the right. So that’s this component here, and subtract from that the size of the force on B due to A, I’m just saying that this forces of equal magnitude to this one. And so that’s this number, minus one times ten to the minus four, giving us negative 7.5 times ten to the minus five newtons per meter. And this is what we expected because there’s some symmetry here, let’s get rid of all these writings here, wire A and wire B have the same currents and have the same distances from other wires with the same currents, so we expected the force on wire B to be equal to the force on wire A but just in a different direction, equal magnitude. And there we have it, the x component is what we expected to be like that, negative 7.5 whereas on wire A, the x component was positive 7.5. And the y component of the force on B will be the same as the y component of the force on A, due to symmetry again and so we have positive 7.5 times ten to the minus five newtons per meter there. And so we have these two forces. We don’t need to do the Pythagorean sum of these components because we have done that already with these numbers, nor do we need to calculate the angle again because we’ve done all that for wire A, and so we’ll say wire B has force of 1.06 times ten to the minus four newtons per meter, 45 degrees above the negative x axis. And so the resultant is this direction and this is the angle here theta, 45 degrees above the negative x axis. Okay. On wire C, well the force on C due to A is the same as the force on A due to C, but just in the opposite direction, so we put in negative five times ten to the minus five newtons per meter. And the force on C due to wire B is the opposite of B on C, and so we have 3.5355 times ten to the minus five, 45 degrees below the negative x axis. And then here’s the new thing that requires calculation, the force on C due to wire D, so these are the bottom two corners. So we have five Amps times five Amps, divided by 0.2 times two times ten to the minus seven, and that gives 2.5 times ten to the minus five newtons per meter. And that is to the right because wire D has a current going into the page just like wire C, they are going in the same direction so this is an attractive force between them, so we expect this force to be to the right. And this one is a repulsive force due to this current going out of the page from wire B, and so it’s down to the left. And here is wire A, exerting a repulsive force straight down. So the force on C in the x direction, is the force on C due to wire D which is entirely positive and to the right, minus the sine of 45 times force on C due to B, so we have 2.5 times ten to the minus five minus 3.5355 times ten to the minus five, over root two, which gives 2.3975 times ten to the minus ten newtons per meter, so that’s positive and to the right. And then in the y direction, we have the force on C due to A per length, and then plus the y component of the force on C due to wire B and that’s negative five times ten to the minus five minus 3.5 times ten to the minus five over root two, which gives negative 7.5 times ten to the minus five newtons per meter. So we have a tiny tiny tiny x component to the right and then we have a large y component down. And it turns out since this x component is five order of magnitude smaller than the y component, the force is essentially straight down, the x component is insignificant. So this works out to 90 degrees, so that’s just down. And the magnitude of the force per length on C will be 7.5 times ten to the minus five newtons per meter, when you take the Pythagorean sum of the components, again this one being insignificant, and so we just get the square root of this thing squared, which is itself. And the force on D per length is by symmetry, the same as the force per length on C, and that is 7.5 times ten to the minus five newtons per meter, down. And if you got this far on the video, congratulations. That’s excellent.