Question
Repeat Exercise 22.48, but with the loop lying flat on the ground with its current circulating counterclockwise (when viewed from above) in a location where the Earth’s field is north, but at an angle below the horizontal and with a
strength of .
Exercise 22.48
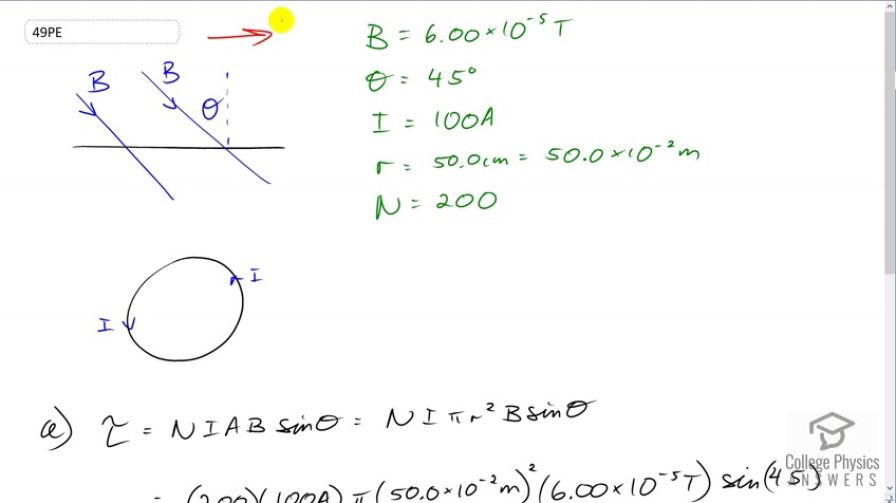
(a) A 200-turn circular loop of radius 50.0 cm is vertical, with its axis on an east-west line. A current of 100 A circulates clockwise in the loop when viewed from the east. The Earth’s field here is due north, parallel to the ground, with a strength of . What are the direction and magnitude of the torque on the loop? (b) Does this device have any practical applications as a motor?Final Answer
- This is a very small torque, so it's unlikely to have a practical application. This torque would be able to lift only a 0.27kg weight placed on the loop.
Solution video
OpenStax College Physics for AP® Courses, Chapter 22, Problem 49 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have a side view here of this loop lying flat on the ground. The magnetic field due to the earth is pointing north-ish, by that it's had an angle of 45 degrees to the ground. And pointing into the ground of 45 degrees. And so this angle theta which is between the perpendicular to the loop and the magnetic field lines also is 45 degrees because this is 90 and we have 90 minus 45 here, it gets 45 there. And the top-down view of this loop shows the current going counter clockwise. And so the component of the magnetic field which is parallel to the plane of the loop is what is going to create a torque. And so it's going to be magnetic field directed upwards here like this and this is north. And at this position at the top of the loop, we can point out thumb to the left in the direction of the current. And our fingers point to the top of the page, in the direction of the magnetic field and the palm is facing into the page. And so there's going to be a force into the page there which is going to cause a torque such that it goes into the page at the top. And on the bottom, the thumb points to the right and the fingers still point upwards in the direction of the magnetic field. And the palm is facing out of the page and so we have dots to represent that force coming out of the page there. And so we have the torque on this loop. And the size of the torque we get from number of loops times the current times the area times the magnetic field strength times sine of the angle between the perpendicular to the loop and the magnetic field. And the area is going to be Pi r squared because it's a circle. So we have 200 times a hundred Amps times Pi times 50 times ten to the minus two meters radius squared times six times ten to the negative five Tesla times sine of 45 degrees giving us 0.666 Newton meters. And this is a very small torque and so it's unlikely to have any practical application as a motor.
