OpenStax College Physics for AP® Courses, Chapter 22, Problem 82 (Problems & Exercises)

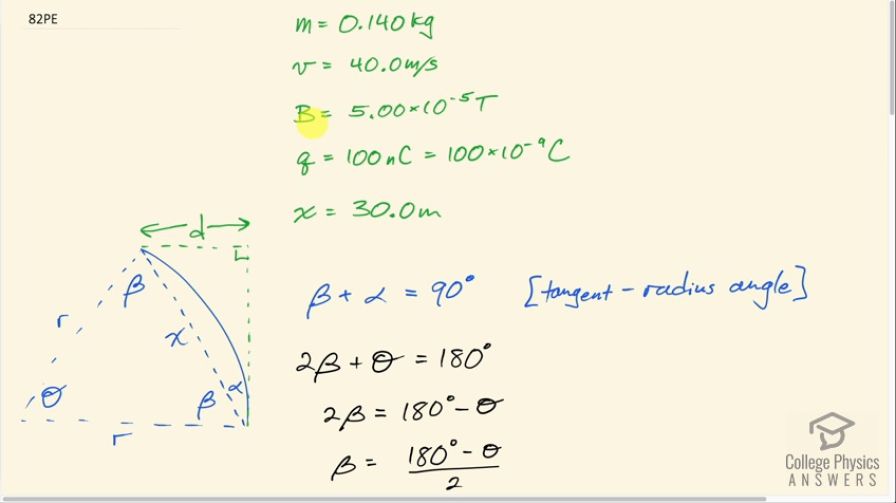
This is College Physics Answers with Shaun Dychko. A 0.140 kilogram baseball is being pitched at 40.0 meters per second perpendicular to Earth's magnetic field, which is 5.00 times 10 to the minus 5 tesla and the ball has a sneaky trick applied where some charge is put on it—100 nanocoulombs— and the ball goes 30.0 meters horizontally and because of the Lorentz Force on the charged ball due to the magnetic field of the Earth, there is some curvature to the ball's path. So I have drawn this in a top-down view; I know that the question said that the Earth's magnetic field is horizontal but I was imagining it being vertical in my mind's eye so I have the field lines for the magnetic field going down the analysis is the same if you want to have Earth's magnetic field horizontal. But in this picture, we have the magnetic field going down, we have the initial velocity of the ball in this direction and if you put your fingers down in the direction of the magnetic field and your thumb pointing up the page... so I should say that the fingers are pointing into the page not down because down is this way and then it gets confusing to say down for those two different directions so we have fingers going into the page, thumb going up and the force will be to the left here and as the direction of the velocity changes, the force will continue to be to the left and we end up with a circular path here, this arc. Okay! So the horizontal distance that the ball travels is 30.0 meters so from this point to this point is this distance labeled x along the dotted line here— that's 30.0 meters— and we are going to examine this picture here of the angles in it and then we are gonna figure out what this radius of curvature is and then knowing the angles figure out what this distance d is this displacement from where it would have gone—had it gone straight— versus where the ball ends up due to following this curved path because of the force applied by the magnetic field on the charge. So if we figure out what α is and we know what x is, we can use sin of α to figure out what d is—the opposite leg of this right triangle. So we know that β plus α equals 90 degrees because I have labeled this angle here β and this angle here is the tangent radius angle, which is always 90, so this dotted line here is a tangent to this curved path and we can also say that 2 times β plus Θ is 180 degrees because this is an isoceles triangle because two sides of the triangle are both radii and so they are of equal length and that means these angles with the base are equal and we'll call them β and then there's this angle here at this vertex we'll call Θ so 2 times β plus Θ is the total angles in a triangle which is always 180 and we can subtract Θ from both sides and get 2β is 180 minus Θ and then solve for β, it's a 180 minus Θ divided by 2 and that's useful because we'll put it in here and figure out what α is in terms of Θ because we are going to be able to figure out what Θ is and then knowing that we will figure out what α is and then knowing what α is and knowing x, we'll figure out d so that's the game plan for this baseball game. So we have 180 minus Θ over 2 substituted in place of β and then divide both those terms by 2 and you have 90 minus Θ over 2 plus α equals 90 and then subtract 90 from both sides and then add Θ over 2 to both sides and now we can say that α is half of Θ. So then we notice that sin of α is the opposite length d that we want to find divided by this hypotenuse, which is x— the horizontal distance traveled by the ball— and then we can solve for d by multiplying both sides by x and say that d is x times sin Θ... or sorry x times sin α I should say and then α we figured out is Θ over 2 so we substitute that in. Then let's figure out what Θ is. Now the definition for Θ in radians— we are using radians here by the way not degrees; I just prefer to do that based on what's happening here, this idea of dividing this arc length by the radius is radians that's the definition arc length divided by radius and so we are gonna take this arc length, divide it by the radius to figure out what Θ is. But we don't strictly know what the arc length is but we do know this chord this straight line distance from this point on the circle to this point and we are going to make an approximation that the chord is the same as the arc length which is true for very, very small angles which this is going to be and we could have verified that by figuring out what r is first and then we would see that it's a very large number and then so given that r is so big and this distance horizontally that the baseball travels is so small in comparison that's going to mean that the angle is small. In this picture that I have drawn, I have drawn this angle way bigger than it would be but I'm doing that just to be able to illustrate things. Okay! So we are going to take this chord approximated as the arc length and divide that by the radius and that's going to be Θ in units of radians. So Θ in radians is arc length of radius, which is approximately equal to—that's what that squiggly equal sign means— the cord length divided by the radius for small chords. So d then is x times sin of Θ over 2; now Θ is x divided by r because the arc length we are approximating is x and we are dividing that by r and we get x times sin of x over 2r. Then we are going to get an expression for r and we know that the centripetal force is always mv squared over r for something moving in a circle at constant speed and that force is being provided by the Lorentz Force, which is the charge multiplied by its speed times the magnetic field strength and we'll solve this for r by multiplying both sides by r over qvB then we get that r is mv over qB. So we are gonna divide by this r when we substitute it in here and when dividing by a fraction, I prefer to multiply it by its reciprocal so that we don't have fractions within fractions so we have xsin of x over 2 multiplied by this flipped over qB over mv and then plug in numbers: we have 30.0 meters times sin of 30 over 2 times 100 nanocoulombs times 5.00 times 10 to the minus 5 tesla divided by 0.140 kilograms times 40.0 meters per second and this works out to 0.402 nanometers— that's a very small distance. So this deflection is not significant; you would not even be able to measure it. So it's not helpful for making curve balls to have the ball statically charged and hope that the Earth's magnetic field will make it deflect.