OpenStax College Physics for AP® Courses, Chapter 22, Problem 86 (Problems & Exercises)

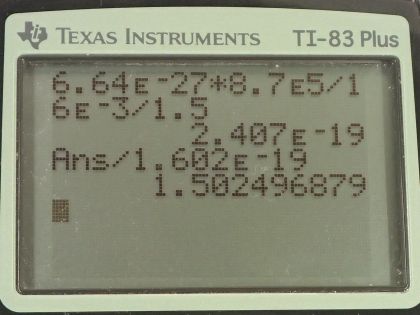
This is College Physics Answers with Shaun Dychko. A particle with a mass of 6.64 times 10 to the minus 27 kilograms is moving at 8.70 times 10 to the 5 meters per second in a circle with radius 16.0 millimeters perpendicular to a magnetic field of 1.50 tesla; we write the radius in meters of course by multiplying by 10 to the minus 3. Now we are going to figure out what is the charge on this particle? So we know the centripetal force is mv squared over r as it is for any particle moving at constant speed in a circle and that equals the Lorentz Force, which is the charge multiplied by its speed multiplied by the magnetic field strength and since the velocity and the field are perpendicular, we don't need to have a sin Θ term here... or factor. So we are gonna solve for q by dividing both sides by vB we end up with q equals mv over rB. So that's 6.64 times 10 to the minus 27 kilograms times 8.70 times 10 to the 5 meters per second divided by 16.0 times 10 to the minus 3 meters times 1.50 tesla and that's 2.41 times 10 to the minus 19 coulombs. Now this is not a realistic answer and it's not the problem that it's small, the problem is that it's not an integer multiple of the elementary charge. So the elementary charge is 1.602 times 10 to the minus 19 coulombs and this charge we found in part (a) when you divide that by the elementary charge, it should work out to an integer not this 1.50... there should be no point here, no decimal besides zero. So because q is not an integer multiple of the elementary charge, it violates this charge quantization, this principle that all charges are multiples of the elementary charge and there's never been an exception ever found to this and so it's accepted as some rule of nature that seems to be obeyed. So in part (c) it asks what was the incorrect assumption that caused this strange answer? And it's not really clear which factor here is the problem because taken on their own, each of these numbers is realistic... you can have magnetic fields this big, you can have a radius of 16.0 millimeters and it's possible to have a mass like this— this is mass of a helium atom— and a speed like this is less than the speed of light so it's possible but taken together, they are not realistic. So either... well, it's really hard to say... maybe the mass and the speed should be higher or the radius and the field should be smaller both of which would increase this charge and well, it has to turn into some multiple of the elementary charge as well.