Question
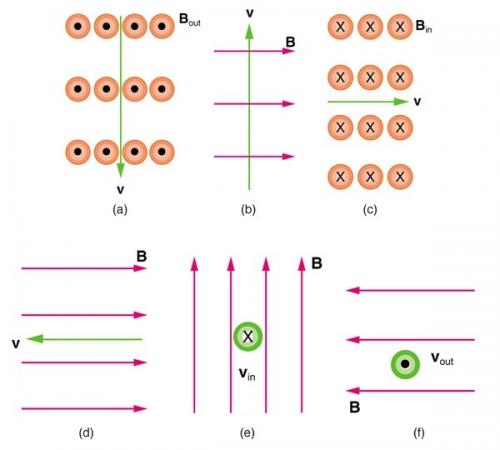
What is the direction of the magnetic force on a negative charge that moves as shown in each of the six cases shown in Figure 22.50?
Final Answer
- right
- out of the page
- down
- no force
- left
- up
Solution video
OpenStax College Physics for AP® Courses, Chapter 22, Problem 2 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. We imagine that this green arrow is pointing in the direction of motion for a negative charge and so it's going downwards and the magnetic field is coming out of the page so with our right hand, we put our thumb pointing down and our many fingers pointing in the direction of these many magnetic field lines coming out of the page and our palm is pointing to the left and that would be the direction of force on a positive charge but in this question, we imagine that this is a negative charge and so the answer is opposite direction to what this right hand rule is telling us; in other words that force will be to the right. So the force will be to the right on this charge so in fact it will go in this curved path like this. Okay! And here we have our thumb pointing upwards in the direction of motion for this charge and our fingers are pointing to the right and our palm is facing down though we have to take our force direction to be opposite to what the right hand rule says since this is a negative charge and so the palm is facing down and so the opposite of that is up and towards us, which will be an arrow with its point coming towards us so just a dot indicates the force coming out of the page towards us. You could also, instead of this opposite business, you could use the left hand rule for negative charges but just... I think that creates more confusion than it solves because then you have to remember which hand am I supposed to use— the right or the left— depending on the sign of the charge so let's just always use the right hand rule and then adjust it for the sign of the charge after. So part (c) our thumb points to the right, our fingers point into the page because these are like the tail feathers of an arrow going away from us so the magnetic field lines are into the page, thumb to the right and then the palm is up but since this is a negative charge, the force direction is the opposite direction which is down instead of up. Here the force is zero no force at all because this Lorentz Force— that's the name for this force on a moving charge due to a magnetic field— is the charge strength multiplied by its speed multiplied by the magnetic field strength multiplied by sin of the angle between the magnetic field and the velocity and in this case, the magnetic field line is pointing to the right— let's draw it in black since I am using red to indicate the force direction— so magnetic field line is to the right and the angle between it and the velocity is 180 degrees so Θ is 180 degrees, the sin of which is zero and so the force is zero. So whenever you have velocity parallel or anti-parallel, as it is in this case, there's no force on the charge due to the magnetic field. In part (e), we have our thumb pointing into the page and our fingers pointing upwards and our palm is to the right but this being a negative charge, the force would be in the opposite direction to that and so it's to the left... the force is to the left. Okay. And then for last one here, thumb out of the page because this is an arrow point coming towards us, fingers to the left in the direction of the magnetic field and the palm is facing down but we will take the opposite of that since this is a negative charge and the force is upwards.