Question
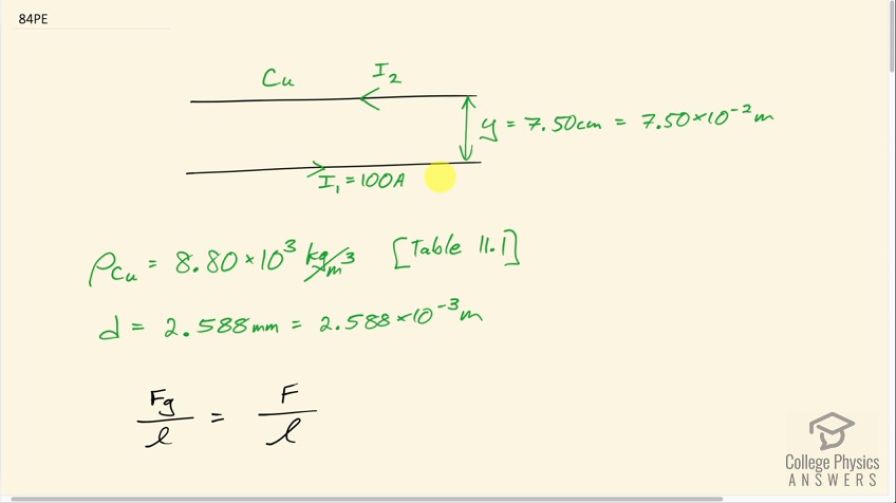
One long straight wire is to be held directly above another by repulsion between their currents. The lower wire carries 100 A and the wire 7.50 cm above it is 10-gauge (2.588 mm diameter) copper wire. (a) What current must flow in the upper wire, neglecting the Earth’s field? (b) What is the
smallest current if the Earth’s field is parallel
to the ground and is not neglected? (c) Is the supported wire in a stable or unstable equilibrium if displaced vertically? If displaced horizontally?
Final Answer
- With vertical displacement the equilibrium is stable since forces will adjust such that a net force accelerates the wire back to its original position. When moving up, repulsion will reduce whereas gravity will not change significantly, in which case there will be a net force due to gravity back down. When moving down, repulsion will increase resulting in a net force back up. With horizontal displacement the equilibrium is unstable since forces will adjust to cause further movement horizontally away form the original position. The wire repulsion will be directly away from the bottom wire, but there will now be a horizontal component pushing the top wire further to the side.
Solution video
OpenStax College Physics for AP® Courses, Chapter 22, Problem 84 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A copper wire is being suspended above this bottom wire that carries 100 amps due to the repulsion between the two currents and this current therefore must be going to the left in this picture if the bottom one is going to the right in order for them to repel, the wire's are separated by 7.50 centimeters and we have to figure out what is this current in the top wire? We know that the density of copper is 8.80 times 10 to the 3 kilograms per cubic meter, which we look up in table [11.1], and we need to know that to figure out what is the gravity per meter on this top wire because the force due to repulsion from the bottom wire has to equal the amount of gravity downwards so we have this repulsion force due to the magnetic field created by the bottom wire and that's a force per length of the top wire and then balancing that is the force due to gravity per length going downwards and we are told that the diameter of this top wire because it's a 10 gauge wire is 2.588 millimeters, and these two pieces of information give us the mass per length. So the force of gravity per length has to equal the repulsion force per length and the force of gravity per length is mass times gravitational field strength divided by the length of the top wire but we don't know what the mass is but we can come up with an expression for it and we can say that it's the density multiplied by the volume of the top wire and that is density multiplied by the length of the top wire times its cross-sectional area this is the volume of a cylinder because if you look at the end of the wire, it will have a circular cross-section and then it will have some length here so some length like this and some radius here and the cross-sectional area will be found by going π times the radius squared. But we are not given the radius, we are given the diameter so we substitute d over 2 in place of r and then this works out to density times length of the wire times π times d squared over 4. Now it's true that we don't know the length but it's gonna not matter because it is going to cancel here because we are finding the force per length and so we substitute all this in for m and then multiply that by g over l and the l's cancel leaving us with density times π times diameter of the wire squared times g over 4. And the force per length of repulsion between two current carrying wires is permeability of free space times the product of the two currents divided by 2 times π times the separation between the wires. Normally there's a letter r here but letter r is a bit confusing because I am using r for the radius of the top wire so I am using the letter y here to say the vertical distance instead. So this repulsion force equals the force per length due to gravity and we can solve for I 2 now so multiply both sides by 2πy over μ naughtI 1. So we end up with π times π is π squared times ρ times d squared times y times g and then divide by 2 because 2 over 4 makes 2 in the bottom times μ naught times I 1 then plug in numbers: π squared times the density of copper in kilograms per cubic meter multiplied by the diameter of the top wire in meters and we square that multiplied by the separation between the wires in meters times 9.81 newtons per kilogram divided by 2 times permeability of free space times the current in the bottom wire, this works out to 1.70 times 10 to the 3 amps. Now we answer the same question again in part (b) but now we include this other element to the problem where there's the Earth magnetic field also producing a force per length on the top wire and we want to find the minimum current that's still needed in the top wire and that means that the force due to the Earth's magnetic field must be upwards to reduce the current required in repulsion between these two wires. So that means the Earth's magnetic field, which is parallel to the ground we are told, has to be coming out of the page towards us and with our current going to the left, the right-hand rule shows that our palm is facing upwards. Okay and the Earth's magnetic field is of magnitude 3.00 times 10 to the minus 5 tesla. So this is the same expression as we had up over... here basically, which then turned into this but there's this additional term which is adding to the repulsion between the wires and the force per length due to the Earth is the current in the top wire I 2 multiplied by the magnetic field due to the Earth so we substitute that in here then we factor out I 2 and we get this bracket and then divide both sides by this bracket and we have the new I 2 and it's the same as it was before except you have this plus B in the denominator although you don't see it the same way the way I simplified this fraction but this is the same as this fraction here if you were to rearrange the factors. Okay! So we have the density of copper times π squared times diameter of the top wire squared times gravitational field strength divided by 4 times permeability of free space times the current in the bottom wire divided by 2π times the separation between the wires plus this magnetic field due to the Earth— 3.00 times 10 to the minus 5 tesla— this is 1.53 times 10 to the 3 amps. Then part (c) asks us is the top wire in a stable or unstable equilibrium if displaced vertically or if displaced horizontally. So vertically speaking, the equilibrium is stable because the forces will adjust during vertical movement such that there's a net force moving the wire back to its original position So if the wire is moved up, there's gonna be reducing repulsion between the wires because it's getting further away from the bottom wire but gravity doesn't change much for small distances when you are so far from the center of the Earth and so there's gonna be a net force downwards because the repulsion which balanced gravity before will no longer do so since it's gonna be reduced and so gravity will have a net force downwards. And if you push the wire down, it will have a net force back upwards pushing it back up where it started since there's going to be an increase in the repulsion. If there is a horizontal displacement however, the equilibrium is unstable because the repulsion is directly away from the bottom wire but now there's going to be some component of this repulsion which is horizontal and that component will further move the wire horizontally. So when a force results from a perturbation from equilibrium that amplifies the perturbation then it's an unstable equilibrium. So vertically speaking, stable equilibrium; horizontally speaking, unstable equilibrium.

