Question
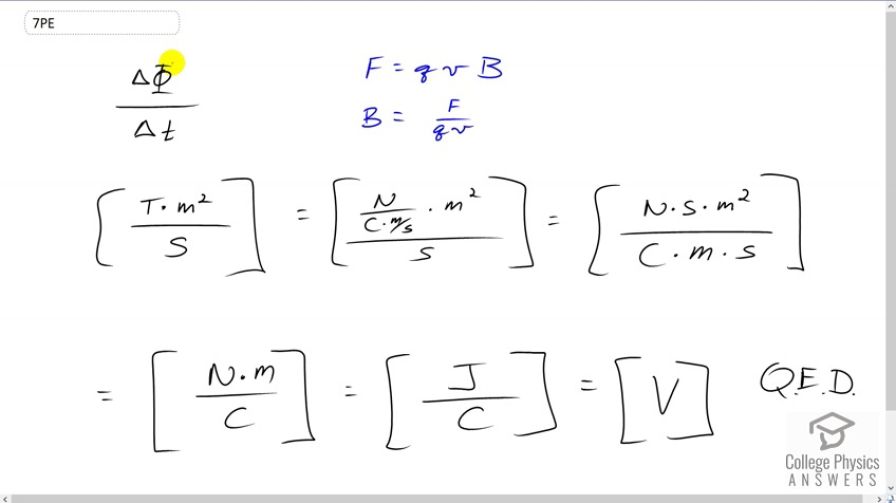
Verify that the units of are volts. That is, show that
Final Answer
See the video solution for dimensional analysis.
Solution video
OpenStax College Physics, Chapter 23, Problem 7 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. Our job is to show that Tesla meters squared per second is the same as volts. So, the rate of change of flux, in other words, we're trying to show that the units of that are volts. So, we know that flux's units of Tesla meters squared because flux is magnetic field strength multiplied by area. So this is Tesla for the magnetic field strength, and meters squared for area. So that's where this comes from. And then, of course, change in time is units per seconds. And then, for the next step, I want to replace Tesla with some more base units. This is one formula that I remember that concludes magnetic field. So, you could've chosen other formulas that include magnetic field. But I have that the force on a moving charge, in the presence of magnetic field, equals a charge multiplied by its speed times the magnetic field strength. And we can solve this for B by dividing both sides by qv. And you get B is F over qV, which means that Tesla is the same as newtons from the force, divided by Coulombs, q, and meters per second from v. And then, we simplify this a little bit. So, this thing here ends up on... we can multiply top and bottom by seconds. So multiply the newtons by seconds, and multiply this denominator by seconds, in which case, it cancels there. So left with newtons, times seconds, times meter squared on the top. And then, multiply this whole top by Coulomb meters, and then multiply the bottom by Coulomb meters, and these Coulomb meters cancel, and then we're left with seconds times, Coulomb, times meters in the bottom. And then, the seconds cancel completely. And meters squared divided by meters is meters. So we have, newtons, times meters, divided by Coulombs. And newtons times meters is Joules, because definition of work is force multiplied by displacement. And so we have newtons times meters, force times displacement, and that makes work, and work is units of Joules. And Joules per Coulomb is the definition of volts. And so, quod erat demonstrandum. Quite easily done. We're finished there.