Question
This problem refers a the bicycle generator which has a 1.00 by 3.00 cm rectangular coil and 50 turns. It is driven by a 1.60 cm diameter wheel that rolls on the outside rim of the bicycle tire. (a) What is the velocity of the bicycle if the generator’s angular velocity is 1875 rad/s? (b) What is the maximum emf of the generator when the bicycle moves at 10.0 m/s, noting that it was 18.0 V under the original conditions? (c) If the sophisticated generator can vary its own magnetic field, what field strength will it need at 5.00 m/s to produce a 9.00 V maximum emf?
Final Answer
Solution video
OpenStax College Physics, Chapter 23, Problem 33 (Problems & Exercises)
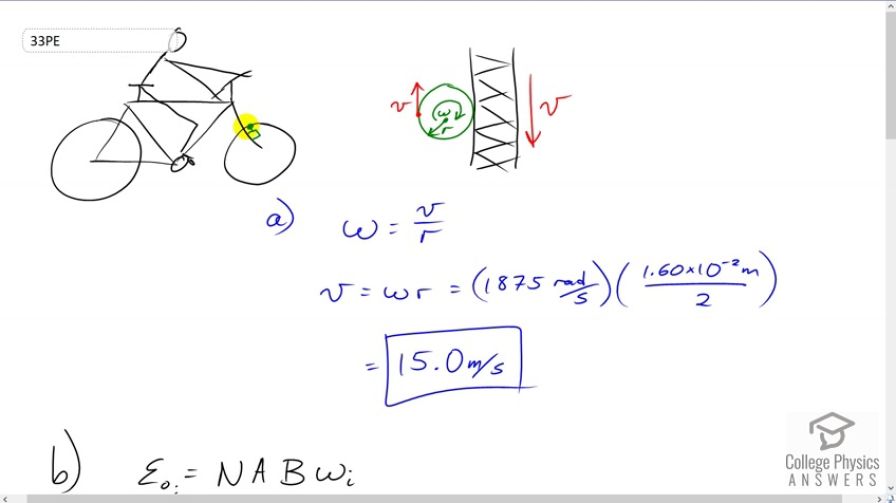
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A bicycle generator is something that attaches to the fork of a bike and it has a small wheel that that touches the tire of the bicycle, and so when the bicycle wheel turns around, it's also turning this little wheel on the end of the generator. And, here is a view looking from the perspective of this cyclist looking down on to the generator. So, if their eyeball is like this, this is the view that we're seeing here. So, this is the top of the wheel attached to the generator and it's rotating around in a clockwise direction as this tire goes down this way. So, we're looking at the tread of the tire. And, a point here on the perimeter of the generator has a tangential velocity equal to the tangential velocity of the tire because they're not slipping, and so they're both moving at the same speed here. And, likewise the other side is also moving at that same speed. So, since we know what the tangential velocity of a point in the perimeter is, we can figure out the angular velocity of this generator wheel. And, we're given its radius as well. So, its angular velocity will be the tangential velocity at this distance R from the center. So, we have V divided by R gives us this angular velocity. And, we'll solve for V by multiplying both sides by R. So, V is Omega times R, and that's 1875 radians per second times 1.6 centimeters which is times 10 to the minus 2 meters, that's the diameter, and we'll have to divide that by 2 to get the radius. And, we get 15.0 meters per second is the velocity of the bicycle. So, it's moving at 15.0 meters per second. That's the linear velocity. Okay. Then, in part B, it says suppose that the bicycle was to slow down to 10 meters per second instead of 15 with the peak Emf change. Well, we know that originally it was 18 volts. And then, we know that the peak Emf is going to be the number of turns in the generator multiplied by the area of the coil inside of it times the magnetic field strength of the magnet inside of it times its angular velocity. And then later on, when its speed changes, it's going to have a different angular velocity corresponding to a linear velocity of 10 meters per second. Whereas, this is the angular velocity corresponding to 15 meters per second. And, the N, the A, and the B do not have subscripts. I didn't put an f, f, f here or an i, i, i because these things don't change. So, there's no need for a subscript on them and that's convenient because they will end up canceling when we divide these two peak Emf's. So, we'll take the final peak Emf divided by the initial peak Emf. That's N A B Omega final divided by N A B Omega initial, and the N A Bs all cancel. Then, we can multiply both sides by the initial peak Emf, which we know is 18 volts. And, that gives us the final peak Emf, which we want to find. It's going to be initial peak Emf times the final angular velocity divided by the initial angular velocity. And so, the angular velocities will be the linear velocity divided by the radius of the generator wheel. And so, we'll substitute this in for Omega F and Omega I. And so, we have peak Emf final is peak Emf initial times the final angular velocity, Vf over R. And then, we're going to divide by Omega I but instead of dividing a fraction by a fraction, we're going to multiply by the reciprocal of this fraction. So, we're going to multiply by R over Vi. And, the R's cancel. And so, we have the final peak Emf is the initial peak Emf times the final linear velocity divided by the initial linear velocity. So, that's 18.0 volts times 10 meters per second divided by 15 meters per second that we calculated in part A. And, we end up with 12.0 volts will be the peak Emf at 10 meters per second. Then in part C, we need to know some information from problem 32, which I haven't solved yet but we can borrow information from it. We know that the coil inside the generator is rectangular and it has a certain length and width. And so, we can use that to calculate its area by multiplying the 1 centimeter length by the 3 centimeter width to get 3 times 10 to the minus 4 square meters area. And, we're told that the coil has 50 turns. And, the magnetic field inside the generator is meant to adjust by itself somehow such that the peak Emf will be 9 volts when going at 5 meters per second. So, at 5 meters per second, it's meant to have 9 volts. So, peak Emf is number of turns times area times magnetic field strength times angular velocity and then we'll substitute V over radius of the generator wheel for angular velocity. And then, we'll solve this for B. And, we'll solve for B by multiplying by R and dividing by N A and V, and we get this line here. We do that in both sides, of course. So, magnetic field strength then is the radius of the generator times the intended peak voltage of 9 volts divided by number of turns times area times the speed of the bicycle. So, that's 1.6 times 10 to the minus 2 meters divided by 2, so the diameter divided by 2, times 9 volts divided by 50 turns times 3 times 10 to the minus 4 square meters area times 5 meters per second, which gives 0.960 Tesla.

