Question
An RLC series circuit has a resistor, a inductor, and a capacitor. (a) Find the power factor at f = 7.50 Hz . (b) What is the phase angle at this frequency? (c) What is the average power at this frequency? (d) Find the average power at the circuit’s resonant frequency.
Final Answer
Solution video
OpenStax College Physics, Chapter 23, Problem 104 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
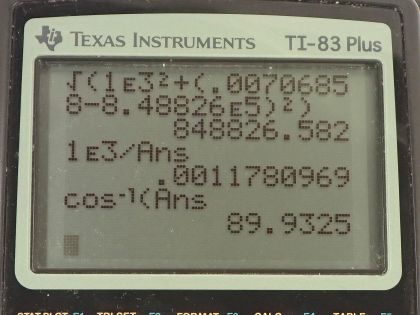
This is College Physics Answers with Shaun Dychko. An RLC-circuit has a 1.00 kiloohm resistor, which is 1.00 times 10 to the 3 ohms, a 150 microhenry inductor, which is 150 times 10 to the minus 6 henries and a 25.0 nanofarad capacitor— 25.0 times 10 to the minus 9 farads— and it says that at a frequency of 7.50 hertz, what is the power factor? So the power factor is cos Φ cosine of this phase angle and that is the resistance divided by the impedance. So the impedance is the square root of the resistance squared plus the inductive reactance minus the capacitive reactance squared so let's figure out what each of these reactances are. The inductive reactance is 2π times frequency time the inductance so that's 2π times 7.50 hertz times 150 times 10 to the minus 6 henries which is 0.00706858 ohms. The capacitive reactance is 1 over 2π times frequency times capacitance so that's 1 over 2π times 7.50 hertz times 25.0 times 10 to the minus 9 farads which is 8.48826 times 10 to the 5 ohms. So the impedance then is the square root of 1.00 kiloohm squared plus this difference squared and this works out to 8.48827 times 10 to the 5 ohms. So the power factor then is the resistance divided by that impedance and this works out to 0.00118 and this has no units because this is ohms divided by ohms. Part (b) is asking what is the phase angle at this frequency and the phase angle is the inverse cosine of this power factor so that's 89.9 degrees. Part (c) is asking what is the average power at this frequency? Now we can't answer this question with a number because we don't know what the RMS voltage is so we are gonna just create an expression for our answer. We know that the RMS current is the RMS voltage divided by impedance and so we can say that the average power then is this substituted for RMS current times the RMS voltage times the power factor and that's V rms squared over impedance times cos Φ. So that's V rms squared— that we don't know— divided by the impedance that we found before multiplied by the power factor this has to be our answer. I suppose we could actually divide these two numbers and get a single factor times V rms squared. Part (d) it's asking what is the average power at the circuit's resonant frequency? Well at the resonant frequency, the impedance equals the resistance since in this formula here, the inductive reactance and the capacitive reactance will be equal—that's what happens at the resonant frequency— and this difference is zero then and so Z is the square root of R squared in other words, Z equals R. And so we have this expression here for the average power at the resonant frequency: it's the RMS voltage—whatever that is—squared divided by the resistance of 1.00 kiloohm.