Question
(a) If the emf of a coil rotating in a magnetic field is zero at , and increases to its first peak at , what is the angular velocity of the coil? (b) At what time will its next maximum occur? (c) What is the period of the output? (d) When is the output first one-fourth of its maximum? (e) When is it next one-fourth of its maximum?
Final Answer
Solution video
OpenStax College Physics, Chapter 23, Problem 37 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
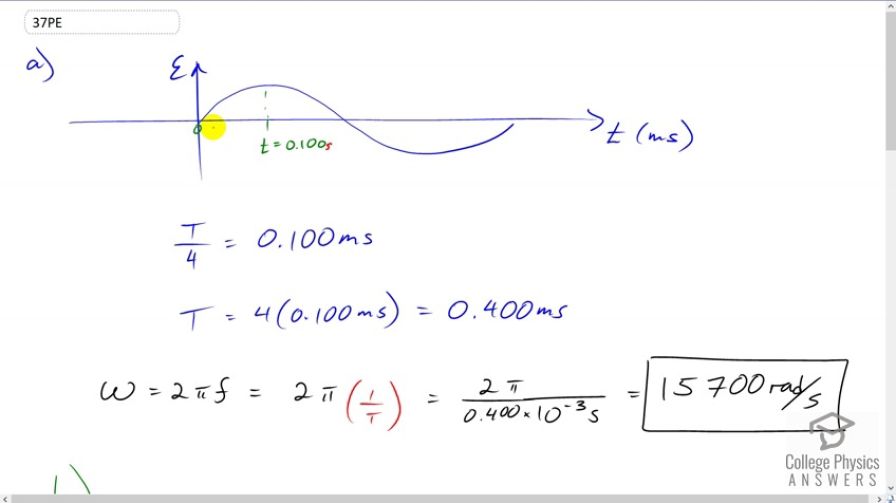
This is College Physics Answers with Shaun Dychko. A coil from a generator that's rotating in a magnetic field is producing an Emf, and we're told that at time zero, the Emf is zero. And, that at some time later, at 0.1 seconds, it increases to a peak Emf. And, this horizontal axis is timed in milliseconds and the vertical axis is Emf. And the question is, what is the angular velocity? Now, we know that the first peak is going to be reached at a time which is 1 quarter of the period, because the period is from here to here. And, this is one quarter of the way to the first peak. And so, we can say period divided by 4. I used a capital T to represent period, not just time, which is lowercase T. So, we have capital T over 4 is 0.100 milliseconds, in which case the period is 4 times that. And so, the period is 0.40 milliseconds. And then, we can use that to figure out the angular velocity, because angular velocity is 2 Pi times frequency and frequency is the reciprocal of period, so we replace F with 1 over T. And so, the angular velocity is 2 Pi divided by 0.40 milliseconds which is 15700 radians per second. And, part B asks us when will the next maximum occur? Well, if we extend this graph a little bit further, this next maximum is exactly one period after the first maximum. So, peaks are always separated by a full period. And, since we know what the period is now, 0.40 milliseconds, we can add 0.40 to the time of the first maximum, which is 0.10 milliseconds, and so the next peak should be at 0.50 milliseconds. So, if we would have put a point on this x-axis that would be 0.500 milliseconds. And part C asks us for the period, which we found in order to answer the other questions, 0.400 milliseconds. Part D says what is the time at which the Emf is one quarter of its peak? So, here's the formula for the Emf. It's the peak Emf times sine of angular velocity times time. And, we're told that it is 1 quarter of the peak, so that's the peak divided by 4. And then, we can divide both sides by Epsilon naught. And, they cancel. And so, sine Omega T is a quarter. And then, we'll take the inverse sine of both sides, giving us Omega T on the left, and inverse sine of a quarter on the right and then divide both sides by Omega, and you are left with the time. So, the time is the inverse sine of a quarter divided by Omega, so that's the inverse sine of one quarter and make sure your calculator is in radian mode. And, divide that by 15708 radians per second which gives 16.1 microseconds. It will be the time when the Emf is one quarter of its peak. Then, we're asked to figure out when will the next time be that the Emf is one quarter of its peak. Now, we can't do our trick of adding a full period to the first answer as we did for part B. For part B, we found the next maximum by adding a period. But for this question, that's not going to work because 1 quarter Emf will occur at this time next, which is not a full period after the first time. So, this T one is our answer from part D, 16.1 microseconds. So, this is 16.1 microseconds and T two will be some other time and it's not going to be a full period after. A full period after would be this time here, which we are not being asked about. We're being asked about this time. Okay. So, I would say when you're taking the inverse trig of a positive number, you're getting a reference angle in the quadrant labeled with the letter A here for all. And so, that's the angle here. This theta here is the whatever inverse sine of a quarter is, that's what this number is there. And then, the next time that sine is a positive in this quadrant, and so we're looking for this angle as our second answer for inverse sine of a quarter. And so, since we have this reference angle here, we can take a full straight line angle which is Pi and then we'll subtract from that this little bit here, which is the same reference angle as we found for part D. And then, that'll be the angle here. So, this is a bit advanced, it requires a whole lesson on how to solve trig functions. There are many many answers to an equation with a trig function so if we have sine of what equals a quarter and the answer is inverse sine of a quarter, it's not quite as simple as just plugging this into your calculator and expecting to get the answer because there are many solutions to this question. There's one here and then there's one here and there's one there and then there's one further on still, and so on. And so, you're always having to ask which solution do I want? And often, when we're just dealing with triangles, the answer is always the first solution that the calculator gives you and that's why when dealing with triangles, you never think about this stuff. But, when you're dealing with more general trig equations, you do have to think about the fact that there are multiple solutions to an equation with a trig function in it like that. So, we have a straight line angle Pi minus the inverse sine of a quarter, which gives us this reference angle and that is the number of radians. We're dividing that by Omega radians per second and that gives us the time of a second time when the Emf is a quarter of its peak. So, that works out to 1.84 times 10 to the minus 4 seconds.

