Question
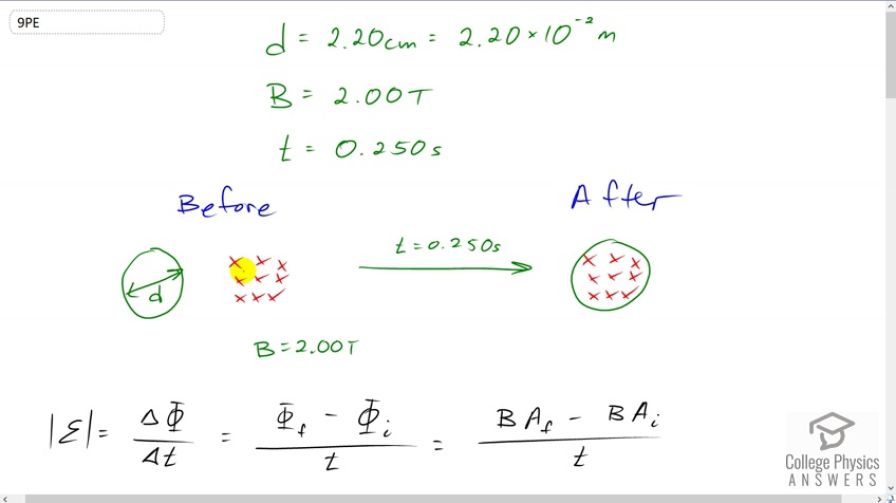
(a) An MRI technician moves his hand from a region of very low magnetic field strength into an MRI scanner’s 2.00 T field with his fingers pointing in the direction of the field. Find the average emf induced in his wedding ring, given its diameter is 2.20 cm and assuming it takes 0.250 s to move it into the field. (b) Discuss whether this current would significantly change the temperature of the ring.
Final Answer
- A temperature change of is insignificant.
Solution video
OpenStax College Physics, Chapter 23, Problem 9 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. An MRI technician has a ring on her finger and the finger is pointing parallel to the magnetic field lines. The magnetic field lines will draw, going into the page, suppose. And the finger is gonna move so that the ring goes entirely into the field in .25 seconds, and the field strength is 2 Tesla, and we're told the diameter of the ring is 2.2 centimeters. So the question is: "how much emf will be induced in the ring due to the changing magnetic flux through the ring?" Because initially, there is no flux because none of the area of the ring has magnetic field lines going through it. And then afterwards, all these magnetic field lines are going through the area. So the induced emf -- and I put absolute value signs around it, just to say that we don't really care about the direction of the emf, we just care about its magnitude -- is going to be the change in the flux per time. And so that's the final flux minus the initial flux divided by time. And that is the magnetic field strength times the final area through which the magnetic field goes, (which is the area of this ring, this circle) minus magnetic field strength times the initial area that the field went through, which is 0 because it's not going through any of the area initially. So the area initial is 0, and the final area that the magnetic field is going through is going to be the area of the circle, pi times radius squared, and we substitute diameter divided by 2 in place of r. So we have pi d squared over 4. And so we plug that into this formula for induced emf, in place of the final area. So we have, magnetic field strength times pi times diameter squared over 4, all over time. So that's pi times 2 Tesla, times 2.2 centimeters written as times 10 to the minus 2 meters squared divided by 4 and divided by .25 seconds. And that gives 3.04 millivolts. So next question is: "will the temperature of this ring increase significantly?" So, we need to figure out how much energy will be deposited in the ring, and then estimate what the ring's mass is and see how much temperature change we expect certain amount of thermal energy to create in this given mass. So, we know that power is energy per time and we wanna solve this for Q, this energy. So we multiply both sides by t. And now this is going to be our heat energy. Now the power is the induced emf squared, divided by the resistance of the ring. Now we're not given the ring's resistance, but we can take a guess at what it might be. We know that resistance of a circular wire is resistivity of the material, so we'll look up the resistivity of gold, which is 2.44 times 10 to the minus 8 ohm-meters. And we multiply by the length of the ring and that is the circumference pi times diameter. And then we divide by the cross-sectional area of the wire. And so, we'll assume that the ring has a circular cross-section with a diameter of, I don't know, 3 millimeters, I suppose. So we can plug all these things in for resistance. So, it's going to be resistivity times pi times diameter, divided by -- this is diameter of the ring, the diameter given to us up here. And then we're going to divide by pi times the cross-sectional diameter of the ring and we'll square that divided by 4 and that comes from here. And then the pi's cancel and you can multiply top and bottom by 4 in which case these 4's cancel there, we're left with 4 times rho times diameter over cross-sectional diameter squared. So it's 4 times 2.44 times 10 to the minus 8 ohmmeters resistivity for gold times 2.2 times 10 to the minus 2 meters diameter of the ring divided by 3 times 10 to the minus 3 meters, cross-sectional diameter squared and this gives resistance of 2.3858 times 10 to the minus 4 ohms. So we can plug that in for resistance here. And we have the voltage that we figured out in part A, and we have the time as well. So that's 3.04 times 10 to the minus 3 volts induced emf squared times .25 seconds divided by this resistance and we get 9.684 times 10 to the minus 3 Joules. So that's how much energy (thermal energy) will be deposited into the ring. So the next question is: "what temperature change will that result in?" Well, we have to guess what the mass of the ring might be. Now, I'm going to make a guess based on what I think the price of the ring might be. So the price of gold, these days, is 38385 dollars per kilogram. And suppose a ring costs 5000 dollars, and it's made out of pure gold; that would make the mass .1303 kilograms because there's 1 kilogram for every 38385, or you know this many dollars times 5000 dollars and the dollars cancel leaving us with kilograms. So we can take this formula for the amount of heat energy that will cause a given temperature change and divide both sides by mass and by specific heat C. And we can look up the specific heat of gold, which is 129 Joules for every kilogram for every Celsius degree. And we are left with Delta T equals Q over mc. So that's 9.684 times 10 to the minus 3 Joules that we calculated earlier, divided by this mass that we've estimated, times 129 Joules per kilogram per Celsius degree, which should result in a temperature change of 5.8 times 10 to the minus 4 Celsius degrees. And this is a very insignificant temperature change.
Comments
why would the cross sectional diameter and the given diameter be different?
Ah, good question. There are two different diameters to consider - the first is the diameter of the circle you would see if you laid the ring flat on a table. This is the diameter given in the question: . For part (b) we're asked about a possible change in temperature of the ring, and to answer this we need to make assumptions about how thick the ring material is. If you were to cut the ring and lay it out as a straight wire and look at one end of the wire then you would be looking at the cross sectional diameter, which I made an assumption to be about .
Hope this helps,
Shaun




