Question
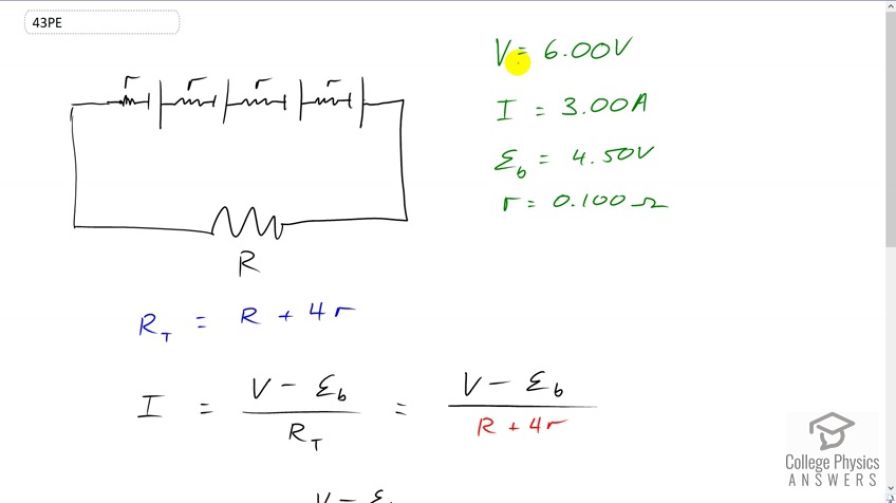
The motor in a toy car is powered by four batteries in series, which produce a total emf of 6.00 V. The motor draws 3.00 A and develops a 4.50 V back emf at normal speed. Each battery has a internal resistance. What is the
resistance of the motor?
Final Answer
Solution video
OpenStax College Physics, Chapter 23, Problem 43 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A toy car is powered by four batteries each of which has an internal resistance of 0.1 ohms. And we're told that the batteries have a voltage of six volts and there's a back EMF in the toy car of 4.5 volts and the current flowing through the circuit is three amps. And the question is what is this resistance R of the motor? Now the total resistance since these are all in series is going to be the resistance of the motor capital R plus four times the little r. So each of the four internal resistances added together and we'll figure out what we can calculate the current as the difference in the voltage applied by the batteries minus the back EMF from the motor divided by this total resistance. And then we substitute for total resistance here capital R plus for little r and that we're gonna solve this for capital R so multiply both sides by R plus four little r and then divide both sides by current and we're left with capital R plus four times little r equals V minus Back EMF divided by current and then we will subtract four times the internal resistance from both sides and we are left with the resistance of the motor is V minus back EMF divided by current minus four times internal resistance. So that's six volts minus 4.5 divided by three amps minus four times 0.1 ohms which gives 0.100 ohms.
