Question
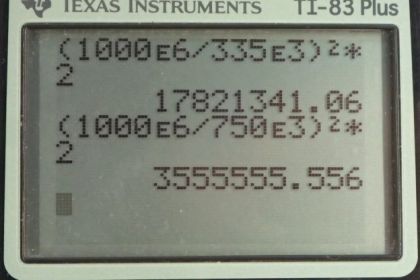
If the power output in the previous problem is 1000 MW and line resistance is , what were the old and new line losses?
Final Answer
Power loss initially is , power loss after a higher voltage is .
Solution video
OpenStax College Physics, Chapter 23, Problem 51 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A power plant is producing 1000 Mega-watt of power say 1000 times ten to the six watt and this power is traveling through electrical transmission lines with resistance two ohms and the initial voltage we’re comparing is 335 kilo-volts and we are comparing that to a final voltage of 750 kilo-volts and we’ll notice power lost in this scenario with higher voltage is much less which is the reason why long distance transmission lines are at high voltage because it reduces the current that’s necessary through them and therefore thought the power lost because the power lost is current traveling through the power lines squared multiplied by the resistance of the lines. Now, we need to figure out what this current will be and so the total power, it has t for total there is going to be current multiplied by the voltage of the power plant and so we can solve this for I by dividing both sides by V and so the current is total power delivered divided by voltage and so the loss then if we substitute this for the current and then square that multiplied by R. So, in initial case we have 1000 mega-watts, this is watts here, and we divide that by 335 kilo-volts, multiplying by and squaring that ratio and multiplying by two ohms and we 17.8 ohms mega-watts of power is lost in the lines and then in the seconds case when we have 750 kilo-volts in the denominator, we end up with 3.56 mega-watts and that’s a very big difference, very big savings in loss by having a higher voltage.