Question
An RLC series circuit has a resistor, a inductor, and an capacitor.(a) Find the circuit’s impedance at 120 Hz. (b) Find the circuit’s impedance at 5.00 kHz. (c) If the voltage source has , what is
at each frequency? (d) What is the resonant frequency of the circuit? (e) What is at resonance?
Final Answer
- At ,
At ,
Solution video
OpenStax College Physics, Chapter 23, Problem 101 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
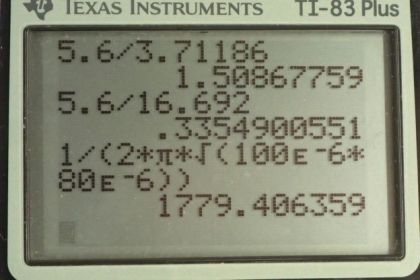
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have an R L C circuit, with a resistance of two and a half ohms, inductance of 100 microhenries and a capacitance of 80 microfarads. And in part A, we need to find the impedance of the circuit when the frequency is 120 hertz. And then in part B, the frequency will be five kilohertz. So, let's figure out how to use this inductance and capacitance in our impedance formula. So, impedance is square root of resistance squared plus the inductive reactants minus the capacitive reactance squared. And so, the inductive reactant is two pi times frequency times inductance and the capacitive reactant is one over two pi times ferquency times capacitance. And so, we can substitute for each of those in our impedance formula. So, we have that the impedance is square root of R squared plus two pi times frequency times inductance minus one over two pi times frequency times capacitance and then square that difference. So, for part A, we have square root of two and a half ohms squared plus two pi times 120 hertz times 100 microhenries, which is times ten to the minus six henries, minus one over two pi times 120 hertz times 80 times ten to the minus six farads. And, this difference is squared. And then, we get 16.7 ohms is our impedance. Now for part B, everything is the same except we have five times ten to the three hertz substitute for the frequency instead of 120 hertz. And this works out to 3.71 ohms. And part C asks us to find out what is the RMS current going through the circuit at each frequency. And so, it's going to be the voltage divided by impedance. So, at five kilohertz, the current will be the 5.6 volts divided by the impedance that we calculated at five kilohertz, which is 3.71186 ohms, for a current of 1.51 amps. At 120 hertz, the current will be 5.6 volts divided by the impedance we calculated in part A, 16.692 ohms, which is 0.335 amps. In part D, we're meant to find out what is the resonant frequency so that's one over two pi times square root of inductance times capacitance. So, that's one over two pi times square root of 100 microhenries times 80 microfarads, which is 1780 hertz. In part E, it asks us what is the RMS current at resonance. At resonance, the inductive reactants equals the capacitive reactants. So, because those are equal, this difference is zero, in which case the impedance is the square root of R squared, which is R. And so, the RMS current at resonance is going to be 5.6 volts divided by the resistance of 2.5 ohms, which is 2.24 amps.