Question
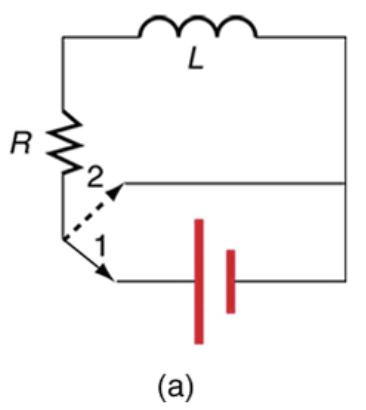
The 5.00 A current through a 1.50 H inductor is dissipated by a resistor in a circuit like that in Figure 23.44 with the switch in position 2. (a) What is the initial energy in the inductor? (b) How long will it take the current to decline to 5.00% of its initial value? (c) Calculate the average power dissipated, and compare it with the initial power dissipated by the resistor.
Final Answer
- . The power dissipated initially in the resistor is greater than the average power dissipated by the circuit by a factor of
Solution video
OpenStax College Physics, Chapter 23, Problem 76 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We are told that this switch in the circuit is in position number two so there's no battery involved at this point in time and the current at this point in time in the beginning of our analysis is 5.00 amps and the inductance is 1.50 henries and this resistance is 2.00 ohms and part (a) asks what is the energy stored in the inductor? The formula for that is one-half times inductance times current squared so that's one-half times 1.50 henries times 5.00 amps squared, which is 18.8 joules. And then part (b) is asking how long will it take the current to decline to 5 percent of this initial value? So the current after sometime divided by the initial current is 5 percent or 0.0500. The current as a function of time is the initial current I naught times e to the power of negative time divided by the characteristic time constant of the circuit. So we can substitute this in place of I and we do that here in red and the I naught's cancel so we have e to the negative t over τ is 0.0500 and then take the natural logarithm of both sides and then on the left, we have the exponent negative t over τ and on the right we have natural logarithm of 0.0500. Then we multiply both sides by negative τ and we get the time then is negative τ times ln of 0.0500. So τ is the inductance divided by the resistance so we can substitute that in here and so the time then is negative 1.50 henries divided by 2.00 ohms times natural logarithm of 0.0500, which is 2.25 seconds. So part (c) is asking what is the average power dissipated? And that's going to be the average power dissipated in the inductor. So that's going to be its initial energy that it has that we calculated in part (a) minus the final energy it has after 2.25 seconds divided by the time, which is 2.25 seconds. So the final energy is one-half times the inductance times the final current, which we are told is 5 percent of the initial current so 0.0500 times I naught so we substitute that in for I f and the initial energy is just what we had in part (a) one-half inductance times initial current squared so we can substitute for each of these terms and then do that in red here and then factor out the common factors one-half LI naught squared from both of these terms and we have that multiplied by 1 minus 0.0500 squared and all this is divided by Δt. So that's one-half times 1.50 henries times 5.00 amps squared times 1 minus 0.0500 squared divided by 2.25 seconds but we are not going to round it here since this is an intermediate calculation so we have 2.2468 seconds and this is 8.32 watts— that's the average power dissipated in the inductor. We are going to compare this with the power initially dissipated by the resistor. So initially we are told that there's 5.00 amps in the circuit and so we take that current squared, multiply it by the resistance of 2.00 ohms and that is 50.0 watts. So the initial power divided by the average power dissipated in the inductor is 6.00.

