Question
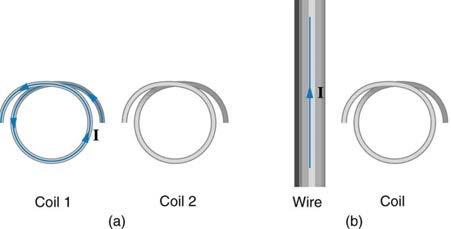
Approximately how does the emf induced in the loop in Figure 23.57(b) depend on the distance of the center of the loop from the wire?
Final Answer
Please see the solution video for details.
Solution video
OpenStax College Physics, Chapter 23, Problem 13 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
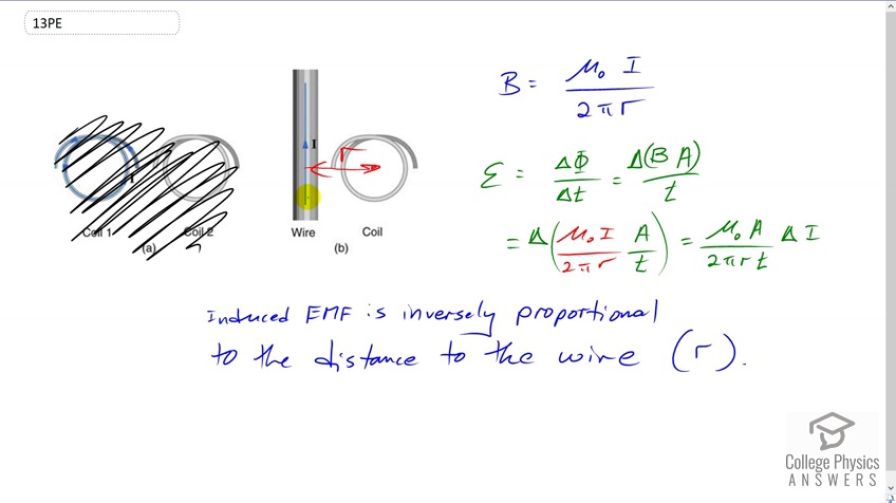
This is College Physics Answers with Shaun Dychko. This question asks us how a change in the distance between the center of the coil and the wire will change the induced EMF. So, the magnetic field due to a current-carrying wire is permeability of free space times the current divided by two pi R, and R is this distance between the coil and the wire. Now, induced EMF is the change in magnetic flux per time. So, that's delta times magnetic field strength multiplied by area of the coil divided by T. We're ignoring angles here because this coil is perpendicular to the field created by this wire. And this is the change in making a substitution for B, is the change in Mu naught I A over two pi R T. The thing that's really going to be changing in this equation is the current. Typically, that's the case. We could imagine that the area could change if the coil was squished or the R could change if the coil was moved further away or closer to the wire. But, let's imagine that it's just the current changing just to establish what effect having the coil at different distances from the wire has on the induced EMF. And so, this can be all thought off as Mu naught A over two pi R T times Delta I, which is a bunch of stuff over we'll just call it Z over R times Delta I. And so, we can see that this induced EMF is inversely proportional to R. It's a whole bunch of things multiplied by change in I divided by R. And so, there we go. As R increases, we would expect the induced EMF to decrease for a given rate of change of current with respect to time.