Question
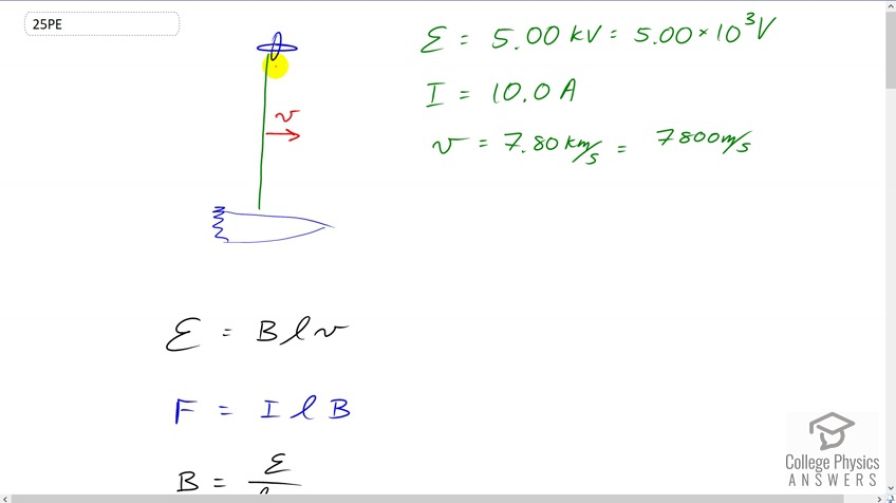
The Tethered Satellite discussed in this module is producing 5.00 kV, and a current of 10.0 A flows. (a) What magnetic drag force does this produce if the system is moving at 7.80 km/s? (b) How much kinetic energy is removed from the system in 1.00 h, neglecting any change in altitude or velocity during that time? (c) What is the change in velocity if the mass of the system is 100,000 kg? (d) Discuss the long term consequences (say, a week-long mission) on the space shuttle’s orbit, noting what effect a decrease in velocity has and assessing the magnitude of the effect.
Final Answer
- 0
- Over a 1 week period the orbital radius will by 99% of it's initial distance. This is OK, but over a longer period a decreasing orbital radius would become an issue.
Solution video
OpenStax College Physics, Chapter 23, Problem 25 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
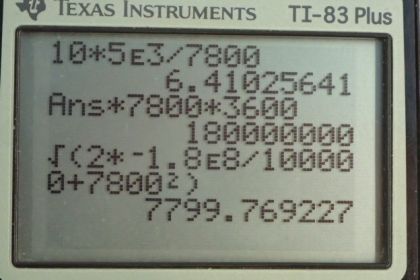
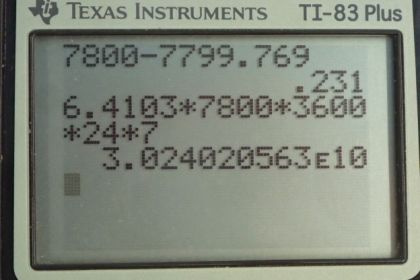
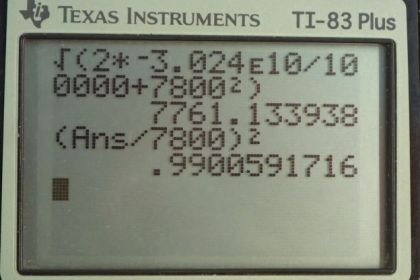
This is College Physics Answers with Shaun Dychko. A satellite is tethered with a conducting wire to a spaceship and both of them are moving to the right, in this picture. And there's a magnetic field -- let's suppose it's downwards -- due to the Earth; that's the Earth's magnetic field. And with a conductor going through this magnetic field, there's going to be an induced emf in the conductor. And that induced emf will be: the magnetic field strength, times the length of the conductor times its speed. Now, we're given the emf and the current, and the speed. And so, we can figure out anything -- we can figure out B, in other words, in this equation here. And we'll use that in our equation for the force on the tether. So the force on a current-carrying wire in the presence of a magnetic field is the current to the wire times its length times the magnetic field strength. So we'll rearrange this formula by dividing both sides by lv to solve for B. And then, plug that in for B in the formula for force. And so I did that here in red. So the force on the tether will be the current times its length times the induced emf divided by its length times its speed. And so, the length cancels and we're left with I emf divided by v. By the way, the current that goes through this wire completes the circuit back to the spaceship by flowing through the charged particles in the ionosphere. Okay? So I thought that was kind of interesting. So, we have 10 amps times 5 kilovolts written as times 10 to the 3 volts, divided by 7800 meters per second (speed of the ship and satellite system). And this works out to 6.41 newtons. So that's not a very large force, but being applied continuously over a long period of time, it actually does result in a large change in kinetic energy of the satellite. So, we're going to find out what is the change of kinetic energy over a period of 1 hour, which is 3600 seconds. And, the change in kinetic energy is going to be the net work done. And that is the force on the tether, times the distance through which that force is applied and the distance that it's going to move is going to be its speed multiplied by time. So we have: 6.4103 newtons times 7800 meters per second times 3600 seconds, gives us 1.80 times 10 to the 8 Joules as the change in kinetic energy. And this will be a reduction in the kinetic energy so you could [unclear] that there is a negative in front of that. And then part C asks: "what will the change in velocity be?" So, change in kinetic energy, instead of being written as the net work done can also be written as the final kinetic energy minus the initial kinetic energy. And we'll solve this for vf. And so we'll add 1/2 mv initial squared to both sides. Like that. A little nicer. And then, switch the sides around as well. And then we have: 1/2 mv f squared equals change in kinetic energy, which we, calculated in part B plus 1/2 mv i squared. And then, we'll multiply both sides by 2 over m. And this works out to vf squared equals 2 times kinetic energy change, divided by mass plus v initial squared. And then we'll take the square root of both sides. And we get the final velocity will be: square root 2 change in kinetic energy over m, plus v initial squared. So let's plug in numbers to calculate what that final speed will be. So that's square root of 2 times negative 1.8 times 10 to the 8 Joules; (it was important to notice that this is a negative change in kinetic energy). And then, divide that by 100,000 kilograms, which we're told is the mass of the whole system I guess, (yeah the system is 100,000 kilograms), and then add to that 7800 meters per second squared, square root that result and you get: 7799.769 meters per second will be the final speed after 1 hour. Now so, finding the change in speed, means you can take the initial which is, well I guess what I've done here is initial minus final, but in any case, the result is gonna be 0. We have 7800 meters per second minus this final speed of 7799.769, which is 0.231 meters per second is the change in speed. That's a reduction and so I guess there should be a negative there and maybe I should've gone final minus initial, like one would normally do. But the bigger point is that this is 0 because these numbers are significant only to the ones place. And this difference, if you round it to the ones place is 0. Now, over an entire week, the change in kinetic energy will be this force times this speed times this period of time. So we're using this net work formula here again. So this is: force times speed times time. And, we're finding the change in kinetic energy over a week. So the subscript w for week. And so, that's the force times 7800 meters per second, times one week converted into seconds, and that works out to 3.024 times 10 to the 10 Joules, in which case, the final speed would be square root of 2 times this change in kinetic energy and then divided by 100,000 kilograms plus the original speed squared which is 7761.13 meters per second. And this is a change that's significant because, you know, it's significant to the ones place and started at 7800 so it's dropped by 39 meters per second almost. Now, we're going to -- well, what was the actual question? We are going to discuss the long term consequences, say a week-long mission, right? So, we have a week-long this change in kinetic energy results in this final velocity. And we're going to see how the radius of its orbit changes as a result of this change in velocity. So, because that's going to be the consequence of slowing down. The consequence is that it will start to have a smaller and smaller orbital radius and then, maybe, get into the thicker atmosphere which will cause it to heat up and perhaps burn and so on. So, centripetal force is m v squared over r, for something travelling in a circle. And the -- we'll have a final radius of orbit and v f squared over force of gravity. And then, an initial radius of orbit, m vi squared divided by force of gravity. And we'll assume that this change in radius is so small that the force of gravity is essentially constant -- even if the radius does change a tiny bit. And so, we'll divide these two radii of orbits. And we get m vf squared over Fg, and then multiply it by the reciprocal of this, instead of dividing by it because it's confusing dividing fraction by a fraction. So we multiply it by the reciprocal of that, and the F g's cancel, the m's cancel, and we're left with the ratio of the velocity squared. And so, we have the final radius, divided by initial radius, will be the final velocity, 7761.13 meters per second, divided by the initial velocity, 7800, and square that ratio, and you get 0.99. So after one week, the orbital radius will be 99 percent of what it initially was. And that's probably okay, but over a much longer period, it would become an issue. And then, eventually, its orbital radius would get smaller and it would heat up as it gets to thicker atmosphere and then that thicker atmosphere would slow it down more, which would, in turn, reduce the radius even more, and then eventually, it would burn up or crash. And there we go.