Question
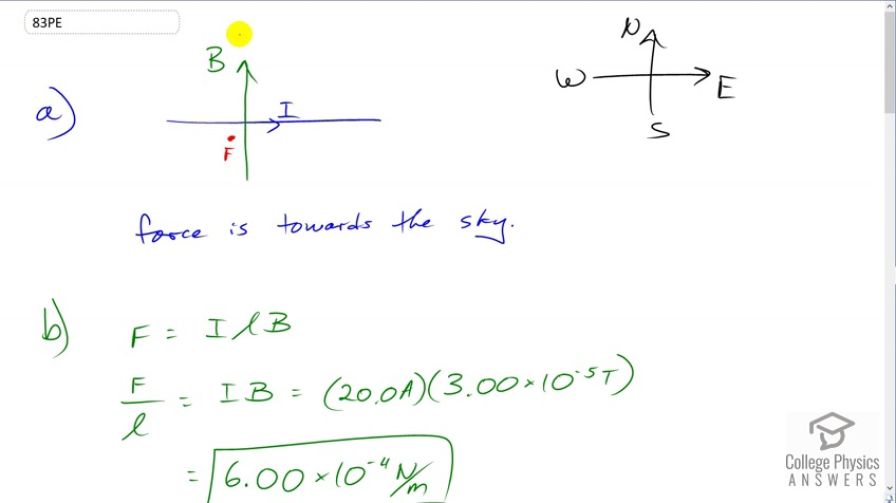
(a) What is the direction of the force on a wire carrying a current due east in a location where the Earth’s field is due north? Both are parallel to the ground. (b) Calculate the force per meter if the wire carries 20.0 A and the field strength is
. (c) What diameter copper wire would have its weight supported by this force? (d) Calculate the
resistance per meter and the voltage per meter needed.
Final Answer
- Towards the sky
Solution video
OpenStax College Physics, Chapter 22, Problem 83 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have a top-down view of this wire and the current is flowing to the East, and the magnetic field of the Earth is going straight North, and they are perpendicular to each other we’re told. So we’ll figure out the direction of the force on the wire due to the magnetic field by pointing our thumb in the direction of the current which is to the right, this is the thumb of the right hand by the way, then our fingers will point in the direction of the magnetic field straight up the page, and our palm is facing in the direction of the force which is coming out of the page, which is towards the sky. Then in part b, we’re asked to figure out what is the force per length. Well the force on the wire is the current through it multiplied by its length multiplied by the magnetic field strength, but we want the force per length and so we divide both sides by L, and we get the force per length is IB. So that’s 20 Amps times magnetic field strength of the Earth, three times ten to the minus five Tesla, which gives 6.0 times ten to the minus four newtons per meter. And in part c, it says what diameter of copper wire would be supported by this force per length due to the magnetic field. Well there’s going to be a weight per length downwards, and there’s going to be the force due to magnetic field per length upwards, and those have to be equal to each other in order to have the thing just hovering there and not accelerating. Now the force of gravity downwards is the mass of this copper wire times g, which is the density of the wire multiplied by its volume times g, and the volume is the cross sectional area of the wire which is pi d squared over four multiplied by its length. Now we want to know what the force of gravity per length is, so finally we have this length factor appearing in our formula and we can divide both sides by it. And we get force of gravity per length is pi times density of copper times its diameter squared times g over four. And we’ll equate this with the magnetic field force per length which is IB that we calculated up here. And we’ll solve this for the diameter. And so multiply both sides by four and divide both sides by pi rho g, and that gives us d squared is four IB over pi rho g, and then we’ll take the square root of both sides and this four is a perfect square so we can take it out of the square root sign and call it two. So d is two times square root IB over pi rho g, so that’s two times the square root of 20 Tesla, oh sorry 20 Amps I should say, that’s the current there. So the diameter is two times square root of 20 Amps times three times ten to the minus five Tesla divided by pi times the density of copper which I looked up on Wikipedia, 8.96 times ten to the three kilograms per cubic meter, times 9.81 meters per second squared, this gives 9.32 times ten to the minus five meters. That’s about 93 micrometers, it’s a very thin wire. Now the resistance per length of this wire will be found using this formula. Resistance of a wire is the resistivity of the material multiplied by its length divided by its cross sectional area. Now we want the resistance per length though so we multiply both sides by one over L, so resistance per length is density, or resistivity I should say. It’s a bit confusing because this rho is used up here to mean density of copper but down here they use the same Greek letter rho in this formula but it means something completely different, it’s the resistivity of the material. So it’s resistivity of copper divided by the cross sectional area of the wire, cross sectional area being pi diameter squared over four. So that’s four rho over pi d squared is our resistance per length. So that’s four times 1.72 times ten to the minus eight Ohm meters, divided by pi times the diameter we discovered in previous part, 9.3227 times ten to the minus five meters squared, giving us 2.52 Ohms of resistance per meter of the wire. Now the voltage per length needed is going to be found using Ohm’s Law, we have V equals IR and if we divide both sides by L, we get V over L is I times R over L, and R over L is what we just found, and so we multiply that by 20 Amps to get 50.4 Volts per meter.

