Question
A velocity selector in a mass spectrometer uses a 0.100-T magnetic field. (a) What electric field strength is needed to select a speed of ? (b) What is the voltage between the plates if they are separated by 1.00 cm?
Final Answer
Solution video
OpenStax College Physics, Chapter 22, Problem 17 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
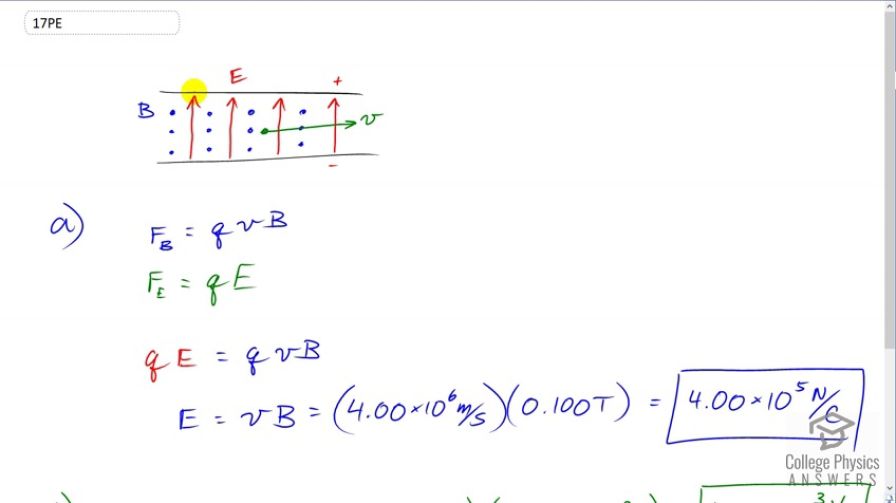
This is College Physics Answers with Shaun Dychko. A velocity selector looks like this where you have two charged plates with an electric field between them. And suppose the electric fields is directed upwards, the direction of force on a positive charge would be in the upward direction and there's going to be a magnetic field pointing towards us. These are the arrow tips, these dots are arrow tips of an arrow coming towards you. And using Right Hand Rule, pointing your thumb in the direction of the velocity of this positive charge, and fingers pointing out of the page, your palm is directed downwards. And so the force due to the magnetic field is down whereas the force due to the electric field is upwards. Now, in order for this forces to be of equal magnitude, we would need the force due to the magnetic field which is qvb equal to the force due to the electric field which is q times the electric field strength. And that will happen only at a certain velocity because this force to due to magnetic field depends on velocity. So we can equate qe with qvB and we divide both sides by q. We end up with the electric field strength is the speed times magnetic field strength. So that's four times ten to the six meters per second times 0.1 Tesla which gives us 4.00 times ten to the five newtons per Coulomb. That's the electric field. Now the voltage between the plates assuming a separation of one centimeter is going to be that electric field strength times one times ten to the minus two meters which gives 4.0 times ten to the three Volts.