Question
Since the equation for torque on a current-carrying loop is , the units of must equal units of . Verify this.
Final Answer
see solution video for dimensional analysis.
Solution video
OpenStax College Physics, Chapter 22, Problem 45 (Problems & Exercises)
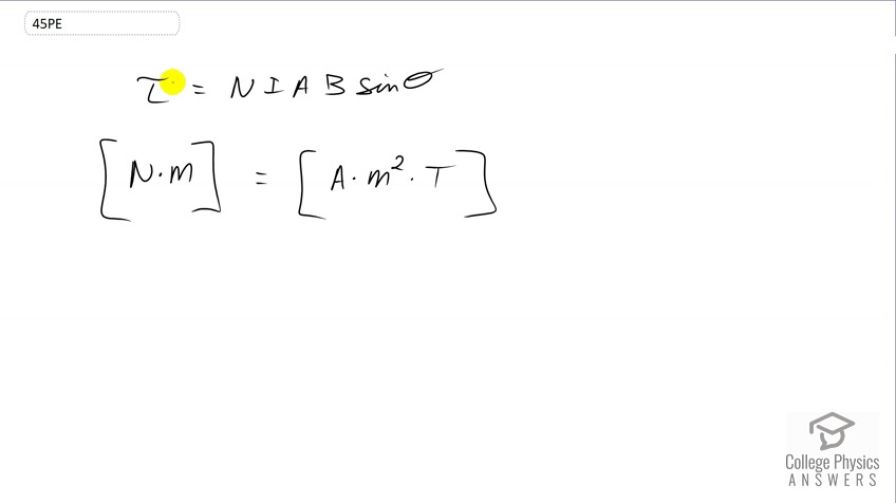
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. We're going to show that the units on the left on the right hand side of this equation are the same and which has to be true for every equation that's correct. So we have torque units, we break it down into newtons and meters and we know it's Newton meters because another formula for torque is that it's force times lever arm. And force with newtons and lever arm's meters with Newton meters there. And on the right hand side, we want to turn everything into newtons and meters if we can and we'll show that this works out to Newton meters. Now it could reduce the Ampere units into Coulombs per second but I got to leave it as Amperes for a minute because I have a feeling that when we break down this Tesla unit and it's going to have an Ampere up here, and which is going to cancel with this one. So, now think about this formula: F equals qvB sine theta. I'm looking for a way to turn Tesla into a more basic type of unit. And so magnetic field is force over qv sine theta. And so the units here are Teslas, are newtons and the force per Coulomb which isn't really a unit. It's more like a counting unit than anything times meters per second times sine theta which also is dimensionless. So, we have newtons per meter per second. And this is Newton seconds per meter. On the other hand, let's keep the Coulombs here. Let's use those Coulombs from the charge because that Coulomb per second, that actually makes Amperes. That's helpful because this works out to newtons per Amp times meters. So instead of Tesla, I'll replace that with newtons per Amp meter. And here is the ticket because the Ampere's cancel and so does one of the meters, leaving us with Newton meters. And so we have verified that the units on the right hand side, here are the same on the units on the left.