Question
A current balance used to define the ampere is designed so that the current through it is constant, as is the distance between wires. Even so, if the wires change length with temperature, the force between them will change. What percent change in force per degree will occur if the wires are copper?
Final Answer
Solution video
OpenStax College Physics, Chapter 22, Problem 79 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
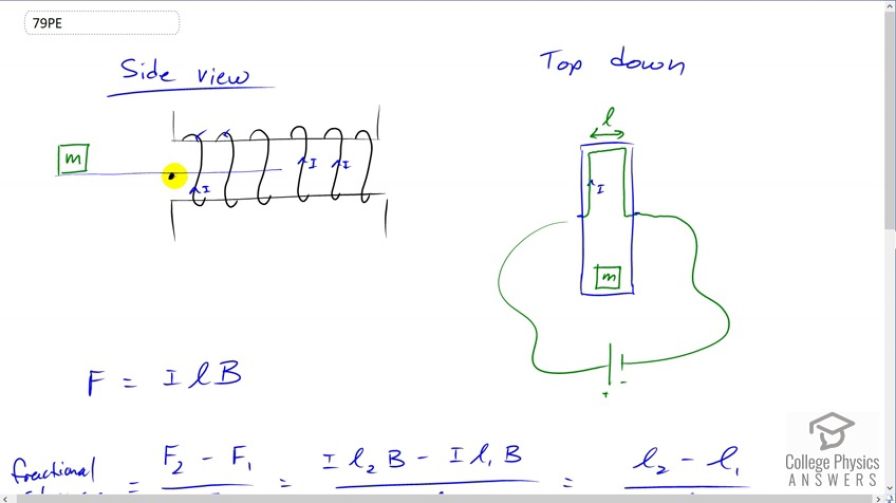
This is College Physics Answers with Shaun Dychko. Here's a side view of what a current balance is. It's a little platform here, which is balance on a pivot here at the edge of a solenoid. And there's a mass put on one end and there's a compensating force downwards on this end due to a magnetic field to plank force on a current-carrying wire there. Now to see how that comes about, we should look at this top down picture of the same thing. So this is the pivot that's here and we're looking at this little platform at the mass it's resting on and here's the mass. And at this end, we see that a wire that is connected to a battery at the pivot goes along one edge of this platform and then goes across the platform here over a length l. And then back along here to the other pivot and goes back to the battery to complete the circuit. And there's a force being applied on this segment of wire. Now, there's a force being applied on these two segments of wire, as well, but these forces are not important. And we can figure out, just as a good exercise in the Right Hand Rule, what direction the forces will be on each of these segments of wire. So, with the current going up and around like this in the coils, there's going to be a magnetic field produced to the left inside the solenoid. And you can confirm that by grabbing this black wire with your right hand and your thumb should be pointing upwards. And your fingers inside the solenoid will be pointing to the left. And so that's the direction of the magnetic field. And so then in this picture here, the magnetic field is along the plane of this blue platform. And so we can calculate the force on this segment which will be zero because the current and the magnetic field are parallel. But on this segment going across however, point your thumb to the right of your right hand in the direction of the current there. The current is going to the right. And then your fingers will point down the page in the direction of the magnetic field. And then your palm is facing into the page. And so this is a force into the page, this is magnetic force into the page here. And this is a top down view. And so this force is going down in this picture. And so I've drawn that with this red arrow here. This is FB here, force due to the magnetic field. And so it's going down to balance this weight of this mass on the other end of the current balance. So, now the force is going to be applied on this segment here will be the current through it multiplied by the length of that segment, multiplied by the magnetic field strength. And so with temperature changes, this length will change and we want to know the fractional change on the force will be the force after some temperature change occurs minus the initial force divided by the initial force. And so that's Il2B minus Il1B over Il1B. Only the lengths need subscripts because the currents and magnetic field strengths will remain the same even after the temperature changes. And so the I and the B is cancel. And we're left with l2 minus l1 over l1. Now back in Chapter, I think it's 13, it talks about the change in length of a substance with changes in temperature. And that equals the coefficient of linear expansion multiplied by the original length multiplied by the change in temperature. And so this is l2 minus l1, the change in length. And so we can substitute this in place of l2 minus l1. And so that's what we've done here, alpha L delta T and divide that by the original length which is L. So l1 is L in this formula. And the L is cancel, and we have fractional change then as alpha times delta T. Now this question asks us for the change per Celsius degree. And so we can divide both sides by change in temperature. And so we have fractional change in force per degree equals the coefficient of linear expansion of Copper, because we're told the wire is made out of Copper. And that is when we look it up in the data table in Chapter 13, 17 times ten to the minus six inverse Celsius degrees. And so the percent change, we can get this by dividing this by a hundred and that is going to be 17 times ten to the minus four percent per Celsius degree is going to be the percent change of the force per Celsius degree.