Question
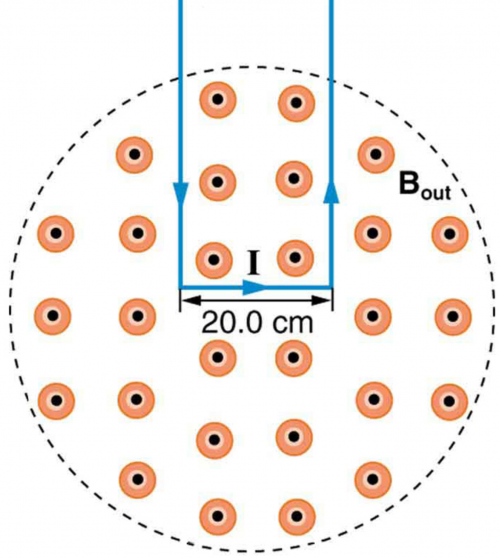
The force on the rectangular loop of wire in the magnetic field in Figure 22.56 can be used to measure field strength. The field is uniform, and the plane of the loop is perpendicular to the field. (a) What is the direction of the magnetic force on the loop? Justify the claim that the forces on the sides of the loop are equal and opposite, independent of how much of the loop is in the field and do not affect the net force on the loop. (b) If a current of 5.00 A is used, what is the force per tesla on the 20.0-cm-wide loop?
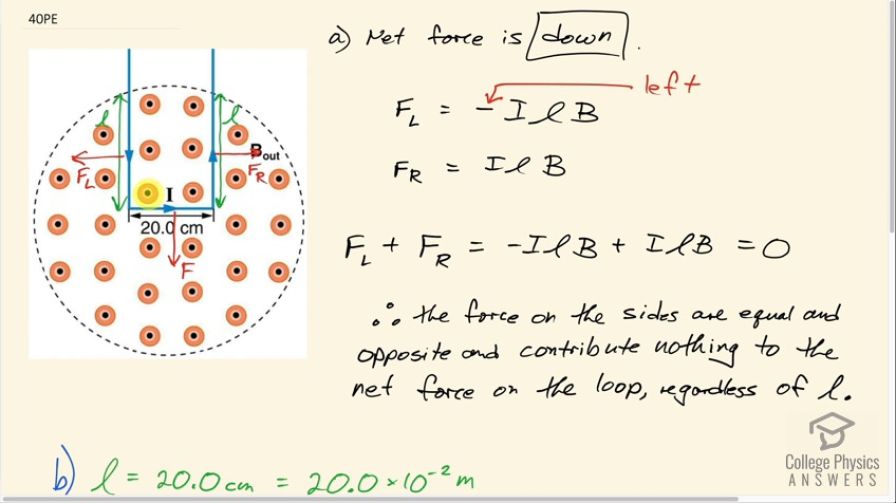
Final Answer
- Net force is down
Solution video
OpenStax College Physics, Chapter 22, Problem 40 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This square loop of wire is in a magnetic field and magnetic field lines are pointing towards us and the plane of this loop is in the plane of the page and is therefore perpendicular to the magnetic field lines. The net force on this loop is going to be downwards because when you use your right hand and put your many fingers in the direction of the many magnetic field lines and you put your thumb in the direction of current, which is to the right in this picture, your palm is pushing a force downwards and so that's the direction of force on this current carrying wire due to this magnetic field. And then we have to consider the left portion of the loop and compare it to the force on the right portion of the loop and compare them and show that they are the same— of magnitudes but opposite directions— so there's some length of wire in the presence of the magnetic field here and that length will be the same for the left and the right side. Now the direction of force on the left side will be towards the left, you put your fingers upwards and your thumb down and your palm will be facing to the left and on the right hand portion, your fingers upwards... or your fingers out of the page, I should say, your thumb towards the top of the page or upwards and your palm is to the right. So these forces are in opposite direction and the magnitude of each force will be the current times the length of wire in the presence of the magnetic field multiplied by the magnetic field strength and the force to the left is gonna get a negative sign to indicate the direction and the force to the right will be positive IlB so when you add them together, you have negative IlB plus positive IlB, which is 0 and so the force on the sides are equal and opposite and contribute nothing to the net force in the loop and it doesn't matter what l is because l will be the same for the two sides and so their forces will still be the same. Now suppose that this bit here of the loop is of length 20.0 centimeters and the current through the wire is 5.00 amps, what is the force per tesla on the wire? So the force on the wire is current times the length times magnetic field times sin of the angle between the current in the field but that's 90 degrees here because the current is to the right and the field is out of the page and we can divide both sides by B to get the force per tesla. And that will be 5.00 amps times 20.0 times 10 to the minus 2 meters times sin 90, which is 1.00 newtons per tesla.
