OpenStax College Physics, Chapter 22, Problem 14 (Problems & Exercises)

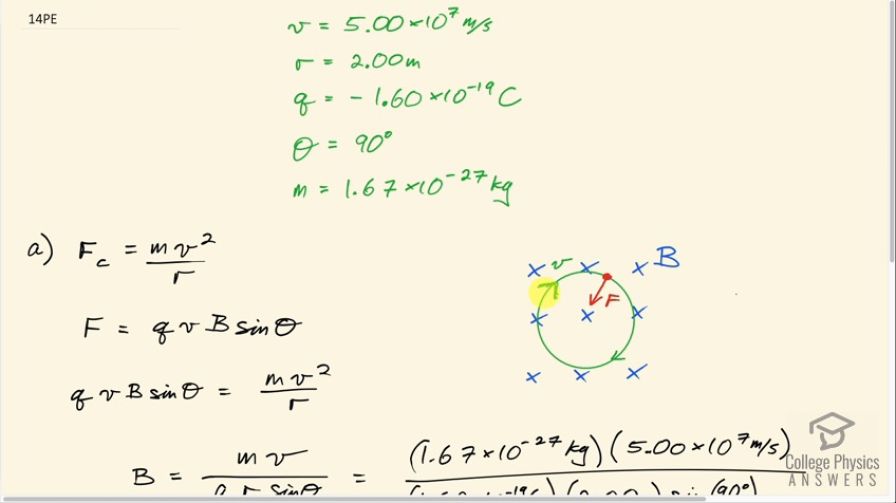
This is College Physics Answers with Shaun Dychko. So we imagine that some anti-matter protons are being stored in a spaceship and they are going to be extracted as needed to annihilate with some regular matter protons to produce energy and the question is what is the magnetic field strength needed in the containment vessel for these anti-matter protons to store them before they need to be used? So they are going to be stored such that they are moving in a circle and so we are going to figure out what is (b) such that we have anti-matter protons moving at this speed of 5.00 times 10 to the 7 meters per second and they will be traveling in a circle of radius 2.00 meters so this is a radius of 2.00 meters here. So just to make sure this picture makes sense, let's put our fingers in the direction of the magnetic field, which is into the page, and our thumb will move in the direction of the velocity of these particles— let's consider this position here, particles are moving like that— and you will notice that your palm is facing away from the center of the circle because that's the direction of force on a positive charge but since these charges are negatively charged since they are anti-matter protons, the force is in the opposite direction to the palm so that means towards the center. Okay! And we know that the mass of these anti-matter protons is the same as the mass of a proton because anti-matter is identical to matter except for the charge and so it's 1.67 times 10 to the minus 27 kilograms on a mass of a single anti-matter proton. So the centripetal force on any object moving in a circle is going to be its mass times its speed squared divided by the radius of the circle and this force is being provided by the Lorentz Force in this case which has a magnitude of charge multiplied by the speed of the particle times the magnetic field strength times sin of the angle between the direction of the field and the velocity and this case, the field and velocity are perpendicular to each other because if we took a side view, we would see these magnetic field lines straight down and we would see the velocity straight to the right if we were to tilt this picture such that we bring this one towards us— that's a dot with an arrowhead coming towards you— and move this side of the picture away from you— these are tail feathers— these are not forces or anything I am drawing here, I am just trying to draw the way in which you manipulate this picture to get this one here. So you have the magnetic field down, you have the velocity to the right and these are perpendicular so that's why we can say Θ is 90 degrees. Okay! So we are solving for B, we'll do that by dividing both sides by qvsin Θ and the v squared divided by v is v to the power of 1 so we have the magnetic field strength then is mass times speed divided by charge times radius times sin Θ. So that's 1.67 times 10 to the minus 27 kilograms times 5.00 times 10 to the 7 meters per second divided by 1.60 times 10 to the minus 19 coulombs times 2.00 meters—radius—times sin 90 degrees and that is 0.261 tesla and this magnetic field strength is definitely doable with today's technology; 0.500 tesla is possible with just permanent magnets and you can get even you know 1.25 tesla if you have superconducting coils with electric current through them. There we go!