Question
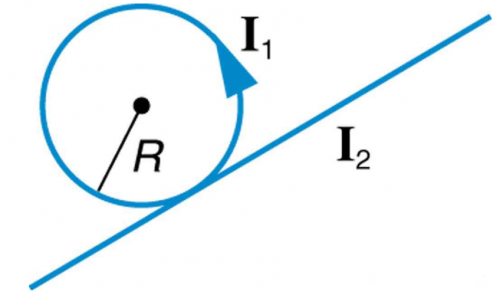
Figure 22.62 shows a long straight wire just touching a loop carrying a current . Both lie in the same plane. (a)
What direction must the current in the straight wire have
to create a field at the center of the loop in the direction opposite to that created by the loop? (b) What is the ratio of
that gives zero field strength at the center of the loop? (c) What is the direction of the field directly above the loop
under this circumstance?
Final Answer
- Left
- The field above the plane of the loop will be somewhat into the page and up the page.
Note: At 4:00 I mistakenly said when describing the formula for the magnetic field above the loop. The formula is written correctly without .
Link to equation: http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/curloo.html
Solution video
OpenStax College Physics, Chapter 22, Problem 68 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. We have a current carrying loop with some radius R and its tangent is a current carrying wire with current I 2 and the question in part (a) is what direction should the current I 2 be such that the magnetic field that this wire produces is in the opposite direction to the magnetic field produced by current I 1. So we have to grab this current I 1 loop with our right hand with our thumb pointing in the direction of the loop and you will find that the fingers are pointing out of the page in the middle of the loop. So that means the magnetic field due to current I 2 has to be pointing into the page in order to be in the opposite direction and grabbing this current I 2 with the right hand with our fingers pointing into the loop here into the page means that our thumb is pointing down into the left so the answer is down to the left for current I 2. Part (b) asks what is the ratio of I 1 to I 2 that gives zero field strength in the center of the loop? So the field due to the current I 1 is the formula for the current in the center of a loop which is permeability of free space times current I 1 divided by 2 times the radius of the loop and then the field strength due to the long, straight wire is μ naught times current two divided by 2π times the distance from the wire. So the distance from the wire is the radius of the loop here, R, and the field strengths have to be the same— they are in opposite directions but they are the same so they will add up to make zero— and so we can say μ naughtI 1 over 2R equals μ naughtI 2 over 2πR and then multiply both sides by 2R over μ naughtI 2 and you get I 1 over I 2 equals 1 over π. So 1 over π is the ratio of these currents. And then in part (c) we are asked what is the magnetic field directly above the loop? So I have a side view here and this current is current I 2 coming directly towards us and this is a side view of the loop and directly above the axis of the loop, we will have the magnetic field due to the loop which is B 1 because it has a subscript 1 since it's being created by current 1 in the loop— it's directly upwards— and the magnetic field due to the wire will be at a right angle to this line connecting this point to the wire. And if you grab this wire with your right hand with your thumb coming out of the page, your fingers at this point will be curling down into the left so this is a right angle here. So what is the resultant of these two? Now we don't need to do a calculation with numbers, we can just get a sense as to whether it's down into the left or up into the left; those are the two possibilities so far at this point considering this picture because we have one vector upwards and the other vector is down and to the left but we don't know how the y-component of B 2 compares with B 1. So B 1 is μ naught 2π times the radius of the loop squared times the current in that loop I 1 over 4π times the distance above the loop along this central axis plus the radius of the loop squared to the power of 3 over 2 and I got that formula from 'hyperphysics' and there's a link in the final answer for that formula and you can simplify it to μ naughtR squaredI 1 over 2 times Z squared plus R squared to the power of 3 over 2. So that's the magnitude of B 1 B 2... it's the same formula as we were using before for B 2 only R is now this hypotenuse of this right triangle, R prime, and R prime is the square root of one leg squared plus the other leg squared and square root can also be written as bracket exponent one-half so that's what I have written here. Okay! So the y-component of the resultant of these two magnetic fields is going to be B 1, which is entirely in the y-direction minus B 2 multiplied by sin of whatever this angle is here because we want to find the opposite leg of this triangle here and we use sin Θ to get it. So this angle here Θ 2 is going to be the same as this angle in here this is also a Θ 2 because this is 90 degrees as I have shown here and this is also 90 degrees here and so we have two 90 degree angles both containing this common angle here and so these two angles here have to be the same and so that means the sin of these two angles will also be the same. So the sin of Θ 2 is the opposite R over R prime so sin Θ 2 is R over R prime but R prime is Z squared plus R squared to the power of one-half so I am gonna substitute this/ in place of sin Θ 2 and that's what I have written here and we substitute here. So we have Z squared plus R squared to the one-half squared so to speak which is Z squared plus R squared to the power of 1 and copying this here and then take out some common factors so we have μ naughtR over 2 times Z squared plus R squared times R to the power of 1 times I 1 over Z squared plus R squared to the one-half minus I 2 over π. Now I 1 we know from part (b) is I 1 is going to be I 2 over π and we multiply both sides by I 2 here so we can make that substitution for I 1 here. So we do the substitution and then we can factor out the I 2 over π from both of these terms and we end up with this line here and then what's important is whether this y-component of the resultant is up or down and that will be determined on how this compares with this. Well it turns out that this term here will always be less than 1 because we have some number R being divided by R squared plus some other number squared and then square rooted and this will always be less than 1 because this denominator is always going to be bigger than the numerator. So as long as you believe that then you are gonna believe that B y is less than 0 because this difference is gonna be less than zero then since this is less than 1 and the resultant then is gonna have this component B x to the left because B 2 has a left x-component and B 1 has no x-component and then we have just figured out that B y is down so the resultant is down into the left in this picture. Now this picture is a side view so to answer the question what is the field above the loop here? It's down into the left when looking at it from the side, which is into the page and up in this picture. So that's gonna be the answer here: the field above the loop will be somewhat into the page and up the page in this picture here.