Question
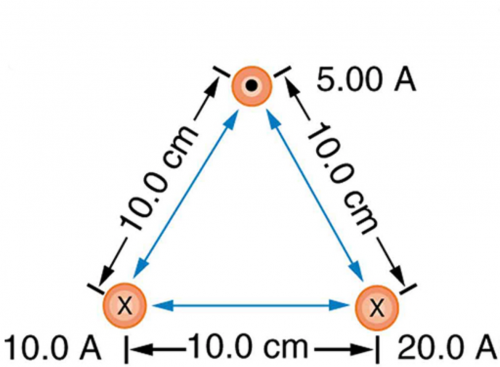
Find the direction and magnitude of the force that each wire experiences in Figure 22.58(a) by, using vector addition.
Final Answer
Wire 1:
Wire 2:
Wire 3:
Solution video
OpenStax College Physics, Chapter 22, Problem 56 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
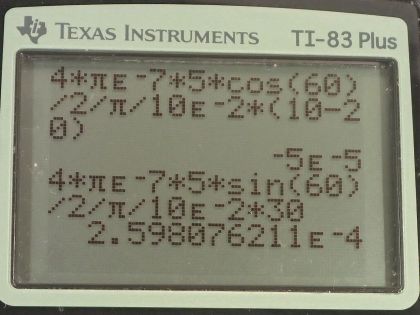
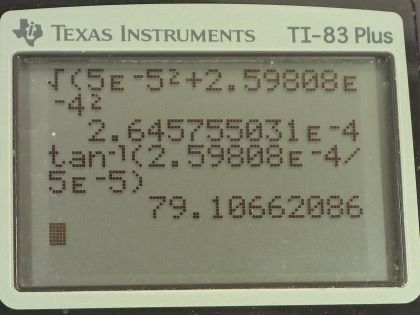
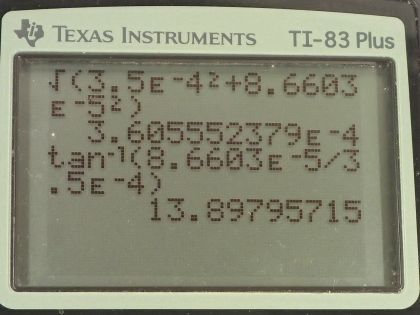
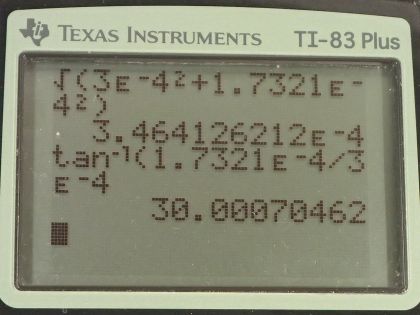
This is College Physics Answers with Shaun Dychko. We have three wires in this problem that are on vertices of a triangle and the triangle has equal length sides— it's an equilateral triangle in other words— and that means the angles in here are all 60 degrees; our job is to figure out what net force each wire experiences and we are gonna be using vector addition to do that. So fasten your seat belt, there's a lot of work to get through here but I think I'll make it clear I hope... let's get going! We have this top wire that we will consider first— we'll call it wire number one— it's gonna experience a repulsive force from wire two up into the right and that's what this vector is here showing— that's the force on wire one due to wire two— and there's also going to be a force up to the left on wire one due to wire three and the force on wire one due to wire three is longer to indicate that the force has greater magnitude because wire three has a 20.0 amp current whereas wire two has only a 10.0 amp current. Okay so these are the two vectors we need to add together and the forces are repulsive because these wires are carrying currents in opposite directions so this is carrying current towards us according to the dot and this is carrying current away from us according to the x; likewise wire two is carrying current away from us. So wire two repels wire one and wire three also repels wire one. Okay! So the x-component of the force per length on wire one is the negative of the magnitude of the force on wire one due to wire three's x-component plus the x-component of the force on wire one due to wire two and something that might be a little bit different than what you see in textbooks or what your teacher might do is I like to put negative signs explicit in my formulas just so that I could take care of them right away; you might see this written and that would be quite correct to say that way and then have the negative sign appear later but I don't like negative signs popping up later, I want to just put it in right away. So this takes cares of negative signs; now I can just think about magnitudes when it comes to the formula for the force. Okay and it's negative because this is the x-component of the force on wire one due to wire three so this is F 13 per l x and this is what we are going to have pointing to the left and we are taking left to be negative. So right is positive and up is positive as per usual standard convention and so that's where this negative sign comes from; this component is to the left. Alright! So how much is it... like how do we find that component? Well, we need to... we need to show that this angle in here is 60 degrees. We can use one of our parallel line rules... this is one line parallel to the base of the triangle and this is the transverse cutting between those two parallel lines and that makes this angle and this angle corresponding angles and corresponding angles are equal— that's one way to say that that's 60. We also need to show that this angle is 60 degrees and the way I look at that is... well, you could do corresponding angles or let's use a different set of parallel line rules... let's say this angle and this angle are interior opposite angles for this transverse and now that we have established that this is 60 since interior opposite angles are equal, these angles are directly opposite and so they are equal as well. Okay! So we have our angles figured out there and this is the adjacent leg of this right triangle here— this vertical leg being the y-component of the force on wire one due to wire three y-component— and so the adjacent leg of this triangle here is found by taking cosine of 60 multiplied by the length of the hypotenuse. So the length of the hypotenuse is... we have a formula for that and we'll multiply it by cos 60 and likewise for the other x-component cos 60 times that hypotenuse gets us this x-component here— this is force on 1 due to 2 x. Okay! Now all these are divided by l because it's force per length; we don't know how long the wires are so we can just say here's how much force there is per meter of wire. So our formula for the force per length between two parallel current carrying wires is the permeability of free space multiplied by the current in one wire multiplied by the current in the other wire and we have currents one and three here because this is the force between wires one and wire three divided by 2π times the distance between the two wires so the distance from wire one to three. I am gonna quickly get rid of these subscripts on the distance between wires because they are all equidistant— these distance between wires is always going to be 10.0 centimeters— so we can simplify our work here by just writing r instead of r 12 or r 13. Okay! So we plug these two formulas in place of the force per length factors here and then we have a lot of common factors and we can factor them out and we end up with μ naughtI 1 so I 1 is common in both terms times cos 60 divided by 2πr times I 2, which is positive, minus I 3, which is negative there and then plug in numbers. So we have 4π times 10 to the minus 7 tesla meters per amp times 5.00 amps times cos 60 divided by 2π times the distance between the wires which is 10.0 centimeters written as 10.0 times 10 to the minus 2 meters multiplied by the current in in wire two, which is 10.0 amps minus the current in wire three, which is 20.0 amps, this works out to negative 5.00 times 10 to the minus 5 newtons per meter and we expected a negative sign because this should be to the left. So that's this part that we just found here. Then... (where was I?) Then we have to find the y-components of these two forces— the total y-component of the resultant vector so we are gonna add the y-component of force on 1 due to 3 and then add the y-component of force on 1 due to 2 and that's gonna be F 12 per l times sin 60 so this is the opposite leg and we find it by multiplying sin of 60 by the hypotenuse and add to that F 13 per l times sin 60— that's the y-component of the force on wire 1 due to wire 3. Okay so then plugging in these formulae for F 12 per l, which we have here and I am rewriting them here factoring out common factors and so we have μ naught times I 1 times sin of 60 over 2πr times I 2 plus I 3 and we have all these numbers here the same as before except you have sin 60 instead of cos 60 and you have 10.0 amps plus 20.0 amps instead of 10.0 minus 20.0 and it works out to 2.59808 times 10 to the negative 4 newtons per meter. Okay! So now we have the y-component of the net force per length on wire one and that's the straight up portion and it's up because it's positive. Then we have the x-component of the force per length in wire one and that's what's indicated here and it's negative so it's pointing to the left and you know, 5 is about... well, this is 5.00 times 10 to the minus 5 and this is something times 10 to the minus 4 so this is like you know almost 10 times smaller so I am just drawing it shorter; this drawing isn't perfectly to scale but the idea is that this is a short x-component and a long y-component... this resultant is what we need to find. So the length of it is gonna be the square root of the sum of the squares of each of these components. So we have the square root of negative 5 times 10 to the minus 5 newtons per meter squared plus 2.59808 times 10 to the minus 4 newtons per meter squared, square root that result and you get 2.65 times 10 to the minus 4 newtons per meter— that's the length of this resultant [force] on wire one. Then the angle Θ 1 is going to be the inverse tangent of the y-component divided by the x-component so the inverse tangent of the opposite divided by the adjacent. So that's the inverse tangent of 2.59808 times 10 to the minus 4 newtons per meter divided by 5.00 times 10 to the minus 5 newtons per meter that gives 79.1 degrees and that's this angle here which is with respect to the negative x-axis above the negative x-axis. Okay! So here is our final answer: 2.65 times 10 to the minus 4 newtons per meter, 79.1 degrees above the negative x-axis. Okay! There's lots of different ways to express angles the standard position way of describing it would be to start from the positive x-axis and go counter-clockwise—this would be the standard position angle. Anyway it will be coterminal with one we have been given and they are both right so you can go 180 minus this number to get the standard position angle. Okay! The important thing is that it's clear what you mean. Then we have wire two in the bottom left corner, it will have an attractive force to wire three and it will have a repulsion from wire one so there's these two forces that we have to add together and wire one is up here—it's a dot coming towards us— and wire three is over here—it's an x with the current going away from us. Current's going the same direction, or attractive, you know, current carrying wires with currents going in the same direction attract each other and that's why this force on wire two is towards wire three. So the x-component then of the force per length on wire two is the negative of force on wire two due to wire one x-component plus the force on wire two due to wire three, which is to the right so it's positive and this requires no trigonometry because it's directly along the x-axis and so I have just μ naughtI 2I 3 over 2π times the distance between the wires whereas for this force on wire two due to wire one per length, it's gonna be in the negative direction and with this part here that we are finding right now... this is force on wire two due to wire one per length x-component and it's the adjacent leg of this right triangle here— this is the right triangle we are looking at— and the x-component is the adjacent leg so we use cos of 60— this is 60 because these are opposite angles— this is opposite to this one— and this one we know is 60 because the interior angles of an equilateral triangle are always 60 degrees and this angle is directly opposite to that angle and so it is also the same, which is 60. Okay! (And then where we at here?) We can factor out a whole bunch of common factors so we have μ naught times I 2 divided by 2πr times I 3 minus I 1 times cos 60 and then we plug in numbers. So that's 4π times 10 to the minus 7 tesla meters per amp times 10.0 amps divided by 2π times 10.0 times 10 to the minus 2 meters and that is multiplied by 20.0 amps minus 5.00 amps times cos 60, this works out to 3.50 times 10 to the minus 4 newtons per meter. Then we want to know the y-component of the force on wire two per length and that will be the y-component of the force on wire two due to wire one plus zero because this force on wire two due to wire three is entirely in the x-direction. And so we have negative permeability of free space times the current in wire one times the current in wire two divided by 2π times the distance between the wires times sin 60, this works out to negative 8.6603 times 10 to the minus 5 newtons per meter. So we take these two components of the resultant and add them as components to find this total you know, the magnitude of the resultant and its direction. So the magnitude of this force on wire two per length is the square root of the sum of the squares of the components. So we have square root of 3.50 times 10 to the minus 4 newtons per meter squared— that's what we found here— and then add to that negative 8.6603 times 10 to the minus 5 newtons per meter squared and we get 3.61 times 10 to the minus 4 newtons per meter and then the direction of this resultant we'll take the inverse tangent of this y-component divided by the x-component and then our answer will be so many degrees below the positive x-axis. So it's the inverse tangent of the y-component per length divided by the x-component per length and that's 13.9 degrees. So our final answer for the force on wire two per length is 3.61 times 10 to the minus 4 newtons per meter, 13.9 degrees below the positive x-axis. And lastly, we have wire three: it experiences attraction to wire two, repulsion from wire one so wire one is up here, wire two is over here and we have to find the x-component of the force per length on wire three and that will be negative of the force on wire three due to wire two per length— because that is entirely in the x-direction to the left— and add to that the positive x-component of the force on wire three due to wire one this is force on wire three due to wire one per length x-component is this dotted line here and we find that by going cos 60 multiplied by the hypotenuse to find this adjacent leg and substituting in our usual formulas here and factoring out common factors, we have μ naughtI 3 over 2πr times I 1cos 60 minus I 2 and then plug in numbers. So we have permeability of free space multiplied by the current in wire three divided by 2π times the distance between wire one and wire three or wire two and wire three multiplied by 5.00 amps times cos 60 minus 10.0 amps and this works out to negative 3.00 times 10 to the minus 4 newtons per meter. And the y-component will be zero from wire two whereas wire one we have to find the opposite leg of this triangle now... (let's move this over here) and then it's this opposite leg that we want to find now F 3 due to wire 1 y-component per length and this works out to negative— because it's downwards— permeability of free space times the current in wire one times the current in wire three divided by 2π times the distance between the wires times sin 60 and we get negative 1.7321 times 10 to the minus 4 newtons per meter. Then draw a quick picture to sketch what we are dealing with here so we are dealing with a x-component that is to the left— this much... 3.00 times 10 to the minus 4 to the left— and then a y-component downwards about half as much and it's downwards because it's negative here so we have sketched that and then find the magnitude of this resultant force per length and that's the square root of the sum of the squares of the components and that's square root of negative 3.00 times 10 to the minus 4 newtons per meter squared plus negative 1.7321 times 10 to the minus 4 newtons per meter squared and this works out to 3.46 times 10 to the minus 4 newtons per meter. And then the direction will be the inverse tangent of the y-component divided by the x-component; I am saying explicitly that it is just the magnitudes that matter here and I have been doing that all along and I am not putting negative signs into this fraction here because I already understand what the direction of the angle is based on my picture and so negative signs will just you know complicate things unnecessarily. So we have the inverse tangent of 1.7321 times 10 to the minus 4 newtons per meter divided by 3.00 times 10 to the minus 4 newtons per meter and we get 30.0 degrees. So the resultant force on wire three per length is 3.46 times 10 to the minus 4 newtons per meter, 30.0 degrees below the negative x-axis. Now give yourself a pat on the back if you made it this far good job... you have perseverance!