Question
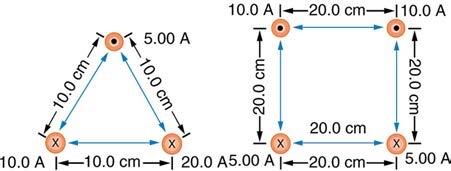
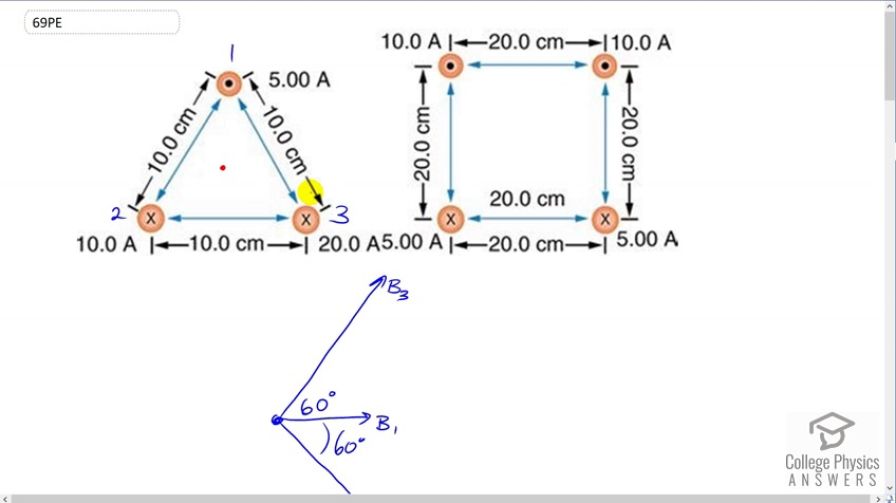
Find the magnitude and direction of the magnetic field at the point equidistant from the wires in Figure 22.58(a), using the rules of vector addition to sum the contributions from each wire.
Final Answer
Solution video
OpenStax College Physics, Chapter 22, Problem 69 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We're going to find the magnitude and direction of the resultant magnetic field here at the very center of this equilateral triangle with these wires that are shown. So that wire number one has a current of five amps out of the page, wire number two has a current of ten amps into the page, and wire three has twenty amps going into the page. All these wires are separated by ten centimeters. Now I've drawn here what the magnetic field vectors will look like from each of the wires. So wire one, when you grab it with your right hand, your thumb points out of the page and at this position here your fingers are pointing to the right. So this is the field from B one. It's going to be the shortest line of all three because this current is only five amps. Let's consider number two. We have our thumb going into the page and then at this position in the center of the triangle your fingers are pointing down and to the right. So this is B two and its length should be twice the length of B one because they're the same distance from this point but wire two has twice the current. Wire three has twice the current of wire two so this line is meant to be two times the length of this line. When you put your thumb into the page at the center of the triangle your fingers are pointing up and to the right. Okay. The next question is how do we figure out these angles of 60 degrees? Well, let's consider wire two being located over here and a line to the center -- there's a triangle there. This line to the center bisects this angle here and this angle is 60 degrees because all the angles in the equilateral or any triangle have to total 180 degrees. An equilateral triangle is going to have three equal angles and so 180 divided by three is 60. This is going to bisect the angle so this is 30 degrees here and then we know that this has to be 90 because the magnetic field is always going to be at right angles to a line from the wire to the point because this is making a circular magnetic field around the wire. Well, another way to say that is to say that we know the magnetic field has to be circular and so the field line will be a tangent to the circle. Tangent radius angle is always 90 degrees. Then we can say that this line and this line -- so this is the horizontal and this is the bottom of the triangle, those are parallel. This angle and this angle are interior angles and interior angles between parallel lines have to total 180. Since this is 90 and this is 30, that leaves 60 leftover for this angle. So 60 and 30 is 90, plus 90 makes 180. There we go, that's why this is 60. You could apply the same reasoning to figure out that this is 60 as well. Okay. So there we've got the angles and now the x component of the resultant is going to be B one which is entirely in the x direction, plus the x component of B two and the x component of B three. That is B two times cosine of 60 because here is the x component of B two and here's the y component of B two. X component is the adjacent leg of this triangle so we use cosine of 60 to multiply by the hypotenuse to get that. Then add to that B three times cos 60, and then for the y component of the resultant we have B three times sine 60 and that's upwards so it's positive, I'm going to take right to be positive and upwards to be positive. Then we'll subtract B two times sine 60 because this component of B two vertical is going downwards and we'll call that the negative direction. Now B one is mu naught I one over two pi r. There's no need to put a subscript on the r, it does not need a subscript one because the distance between each of the wires to the center of the triangle will be the same. But we do need a subscript on the current. We need to figure out what this distance is now from the wire to the center. The way I've drawn my triangle I guess this is wire two and it doesn't matter because they're always going to be the same. So, this vertical from the center of the triangle -- I mean center of the triangle here to here is going to bisect this side because this is an isosceles triangle and the altitude of an isosceles triangle always bisects the long side. So this is five centimeters from here to here, and this is 30 degrees in there, so now that triangle is drawn here. We say that the cosine of this angle is the adjacent over the hypotenuse so we'll solve for the hypotenuse by multiplying both sides by r over cos theta. So r is the adjacent over costheta. So that's five centimeters which is five times ten to the minus two meters divided by cos 30 which is 0.057735 meters. So, B one then is four pi times ten to the minus seven Tesla meters per amp times current one divided by two pi r and the two pi will cancel with two pi from -- well, will cancel with one of the factor two's there. This makes just the number two. So two times ten to the minus seven Tesla meters per amp times five amps in wire one times 0.057735 meters distance from the wire one to the center is 1.7321 times ten to the minus five Tesla. Now magnetic field due to wire two is going to be mu naught I two over two pi r, but current two we can see is two times current one, five amps versus ten amps. So we'll replace I two with two times I one and factor or just move the two outside there. You can see that this is two times mu naught I one over two pi r which is B one. So the magnitude of the magnetic field due to wire two is two times that due to wire one. So we have 3.4641 times ten to the minus five Tesla, the magnitude of the field due to wire two. Then wire three has a current twice wire two and so the magnetic field due to wire three will be two times the magnetic field due to wire two, and we end up with 6.9282 times ten to the minus five Tesla. So now we know what B one, two and three are. So then we substitute those numbers into the component formulas for the resultant and we end up with B x is going to be B one plus B two times cos 60 plus B three times cos 60. This works out to 6.9283 times ten to the minus five Tesla. Then the y component is going to be B three was it? Yep, B three times sine 60 minus B two times sine 60. This works out to three times ten to the minus five Tesla. Then we'll take the Pythagorean sum of those by taking the square root of the sum of the squares of those two components to get the magnitude of the resultant. That works out to 7.55 times ten to the minus five Tesla. So I squared this number and then added it to the square of this number and then took the square root of that sum. The angle will be the inverse tangent of the components. So it's the inverse tangent of three times ten to the minus five over 6.9283 times ten to the minus five. This is 23.4 degrees. We know that's above the positive x axis because we have a picture here. We have the resultant x component is positive so it's to the right, and the resultant y component is positive and so it is up. So the resultant is here . It's going to be this angle that we're finding. It's going to be above the positive x axis. There's the resultant, 7.55 times ten to the minus five Tesla, 23.4 degrees above the positive x axis.