Question
An electron in a TV CRT moves with a speed of
, in a direction perpendicular to the Earth’s field, which has a strength of . (a) What
strength electric field must be applied perpendicular to the Earth’s field to make the electron moves in a straight line? (b) If this is done between plates separated by 1.00 cm, what is the voltage applied? (Note that TVs are usually surrounded by a ferromagnetic material to shield against external magnetic fields and avoid the need for such a correction.)
Final Answer
Solution video
OpenStax College Physics, Chapter 22, Problem 18 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
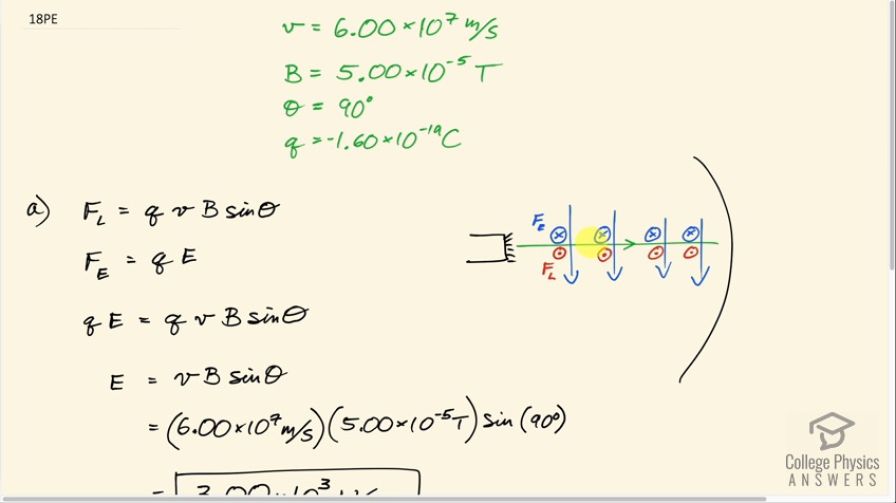
This is College Physics Answers with Shaun Dychko. Let's imagine we have a side view of a cathode ray tube where we have electrons being projected towards this screen of the CRT and so the velocity is indicated by the green arrow to the right, the Earth's magnetic field suppose is straight down in that case, the Lorentz Force or the force applied on the moving charge due to the field will be out of the page and you can verify that by putting your right hand fingers pointing down, your thumb pointing to the right in the direction of velocity of the charge and your palm will be pointing into the page but since this is a negatively charged particle, the force direction will be opposite to the right-hand rule's answer and so the force is actually out of the page and that's why there's a dot here showing an arrowhead moving towards you. So that's the direction of the Lorentz Force and the force due to this electric field that we have to figure out, it has to be in the opposite direction and it's going to be into the page then. So electric field direction by the way is gonna be out of the page but the question doesn't ask for that... it just asks what's the magnitude of the electric field because the electric field direction is the direction of force on a positive charge but since this is a negative charge and we need the force to be into the page and so the electric field is going to be in the opposite direction to the force applied on this negative charge. That part didn't make sense; it doesn't really matter that's just another side point. The important thing is that the size of this electric field force has to be the same as the size of this Lorentz Force and we do verify here though that the electric field direction is perpendicular to the magnetic field direction. Okay! The Lorentz Force is the charge times its speed times the magnetic field strength times sin of the angle between them and because the angle between them is 90 degrees, this sin of 90 will be 1. The force due to the electric field is the charge multiplied by the electric field strength and so we can equate these two because we are told that we want to have the electron moving in a straight line and so that these forces will balance each other and so we can solve for E by dividing both sides by q. So the electric field strength is gonna be the speed times the magnetic field strength multiplied by sin Θ. So that's 6.00 times 10 to the 7 meters per second is the speed of the electron multiplied by the magnetic field strength due to the Earth of 5.00 times 10 to the minus 5 tesla times sin of 90 degrees and that's 3.00 times 10 to the 3 newtons per coulomb. And the next part we are told to imagine that this electric field's being provided by two large parallel plates in which case, the field between them is the voltage between them divided by the distance by which they are separated and so what is the voltage then? We can solve for v by multiplying both sides by d and the voltage then is the electric field— 3.00 times 10 to the 3 newtons per coulomb— times the 1.00 times 10 to the minus 2 meters separating them that is 1.00 centimeters given to us in the question but written as times 10 to the minus 2 and this works out to 30.0 volts. And that's doable certainly but typically, these cathode ray tubes are shielded by ferromagnetic material that will block this external magnetic field so that this compensation is not necessary.
