Question
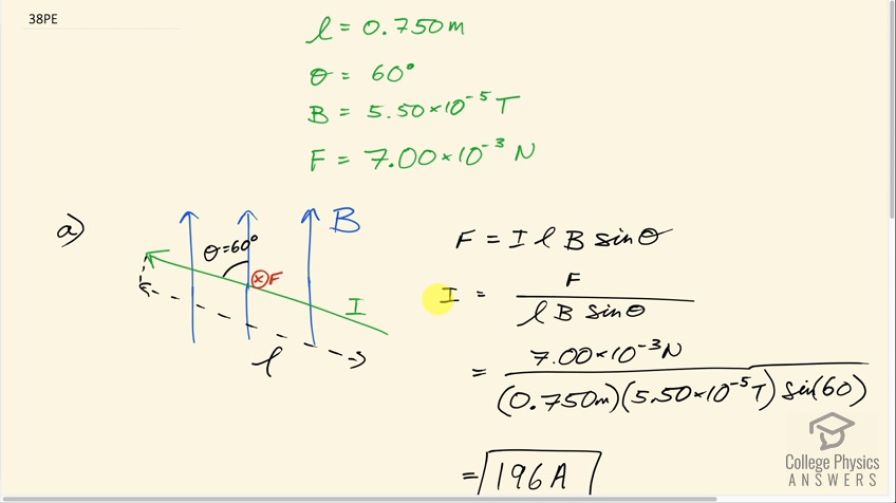
(a) A 0.750-m-long section of cable carrying current to a car starter motor makes an angle of with the Earth’s field. What is the current when the wire experiences a force of ? (b) If you run the wire between the poles of a strong horseshoe magnet, subjecting 5.00 cm of it to a 1.75-T field, what force is exerted on this segment of wire?
Final Answer
Solution video
OpenStax College Physics, Chapter 22, Problem 38 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The current in a wire inside a car going to the car starter is carrying some current that we have to figure out but we do know the force on the wire, which is 7.00 times 10 to the minus 3 newtons, and due to the Earth's magnetic field, which is of strength 5.50 times 10 to the minus 5 tesla and the wire is 0.750 meters long and it makes an angle of 60 degrees to the magnetic field. So this could be a drawing of the wire here where this angle 60 is shown here between the direction of the wire and the direction of the magnetic field and the force according to this picture, if you put your right hand upwards in the direction of magnetic field and your thumb towards the left-ish... towards the current, the palm is facing down and so that will be the direction of force and the force is the current in the wire times its length times the magnetic field strength times sin of the angle between the current and the magnetic field. So we can solve this for I by dividing both sides by lBsin Θ and we get then that the current is the force divided by length times magnetic field times sin of Θ. So that's 7.00 times 10 to the minus 3 newtons divided by 0.750 meters times 5.50 times 10 to the minus 5 tesla times sin of 60 degrees, which is 196 amps. In part (b), we imagine taking this same wire with this current that we calculated and putting it between the ends of a large permanent magnet and these faces of this magnet are of length 5.00 centimeters and the magnetic field between the ends of a permanent magnet like this are all going to be parallel to this axis here connecting the two faces and that means it's gonna be perpendicular to the current here and so we can say Θ is 90 and the magnetic field strength we are told is 1.75 tesla and so we will figure out the force on this wire; it will be the current times its length times B times sin Θ. Now the length of course is not from this corner to this corner, the length is just that portion that is in the magnetic field so that's 5.00 centimeters written as times 10 to the minus 2 meters times 1.75 tesla times sin of 90 degrees times our answer for part (a)— without rounding to avoid intermediate rounding error— and we get 17.1 newtons.