Question
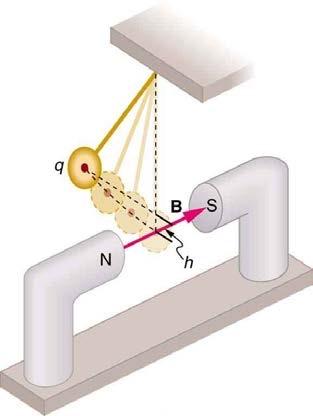
(a) A pendulum is set up so that its bob (a thin copper disk) swings between the poles of a permanent magnet as shown in Figure 22.63. What is the magnitude and direction of the magnetic force on the bob at the lowest point in its path, if it has a positive charge and is released from a height of 30.0 cm above its lowest point? The magnetic field strength is 1.50 T. (b) What is the acceleration of the bob at the bottom of its swing if its mass is 30.0 grams and it is hung from a flexible string? Be certain to include a free-body diagram as part of your analysis.
Final Answer
Solution video
OpenStax College Physics, Chapter 22, Problem 73 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. So we assume that this pendulum bob comes from this initial height here and reaches this point here in the magnetic field. And we assume that it has not experienced any magnetic field until it gets to this final point here at the bottom of its swing. That isn't going to be strictly true because the magnetic field lines that occur out from the north and into the south. And so, the pendulum bob will experience a magnetic force sort of on its way to the bottom of its wing. But we'll ignore that and assume that this magnetic field is really well columnated. Meaning it's existing only in this sort of tube of space between the north and south poles. And that outside of this tube space, it is a really small magnetic field. So, that will mean that when the pendulum bob gets here, it will have a kinetic energy equal to the gravitational potential energy it had on its initial position. So the one half m times velocity at the bottom of its swing squared equals mgh the gravitational potential energy it had at the beginning. And so we could solve this for vb by dividing both sides by m and multiplying both sides by two and then taking the square root of both sides. And you get vb square root two gh. Now the force on this pendulum bob is going to be the force due to the magnetic field on a moving charge. And so we are given the charge of the bob and now we figured out an expression for its speed. And we're told that the magnetic field strength is. And so we'll substitute in square root two gh in place of v. And then we plug in numbers. So the magnetic force is going to be 0.25 micro Coulombs which is times ten to the minus six Coulombs times square root of two times acceleration of the gravity, 9.1 meters per second squared times the initial height of 30 centimeters which is times ten to the minus two meters. And then take the square root of all that and into this the square root sign and then multiplied by one and a half Tesla. And we get 9.09 times ten to the minus seven newtons. And this will be directed up initially because we assume that there's a positive charge in here because we're told the charge is 0.25 micro Coulombs. If it was a negative charge then it would have said negative 0.25 micro Coulombs. But it said 0.25 micro Coulombs with a positive charge and so we're going to point our thumb in the direction of its motion which is this way. And then point our fingers in the direction of the fields which goes from the north towards the south. And our palm will be for it's facing upwards in the direction of the force. So, that's part a and then part b, we have to figure out what the acceleration of this pendulum bob will be at the bottom of its swing. So here's a free body diagram showing the three forces involved. There's the force of tension due to the string connecting the pendulum bob to the pivot of the top there. There is this magnetic force that we calculated. And there is the weight downwards. So before this pendulum bob reaches the field, the tension upwards has the equal the weight downwards. And so the tension is going to be mg. And this is immediately before the field and just after entering the field, we're going to introduce this additional force due to the magnetic field upwards and we're going to assume that since this pendulum bob has just entered the field that the tension force hasn't change compared to what it was before the field. Now after a moment of time, that won't be true anymore because the tension will reduce because there's this upwards force due to the magnetic field. Tension is only as strong as it needs to be to avoid having the string stretched too much. Now since this string is flexible though, we can assume that, I think that's why they added that detail to the question, that saying that the string is flexible which is to say that even after this magnetic field forces being sorted upwards, the string has some elasticity to it. And so it will continue to exert a force upwards even as it starts to recoil. So, that means the net force is going to be just the magnetic force since tension force and gravity of b of equal magnitudes and we'll divide both sides by m to solve for A. And so that's 9.0933 times ten to the minus seven newtons divided by 30 grams which is 3.03 times ten to the minus five meters per second squared upwards.
